Question

【题目】解下列不等式（组）
（1）2x2﹣3x﹣5≥（ ）x+2
（2） ．

Answer 1

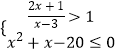【答案】
（1）解：2x2﹣3x﹣5≥（ ）x+2等价于x2﹣3x﹣5≥﹣x﹣2等价于x2﹣2x﹣3≥﹣0，

即为（x﹣3）（x﹣1）≥0，解的x≥3或x≤1，

故不等式的解集为（﹣∞，﹣1]∪[3，+∞）

（2）解： ＞1，即为 ＞0，即为（x+4）（x﹣3）＞0，解得x＜﹣4，或x＞3，

x2+x﹣20＜0，即为（x+5）（x﹣4）≤0，解得﹣5≤x≤4，

故原不等式组的解集为[﹣5，﹣4）∪（3，4]

【解析】（1）先根据指数函数的单调性，得到x2﹣3x﹣5≥﹣x﹣2，再利用因式分解即可求出不等式的解集；（2）分别求出每个不等式的解集，再其交集即可得到不等式组的解集．