题目内容
【题目】在矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,则在翻折过程中,异面直线
折起,则在翻折过程中,异面直线![]() 与
与![]() 所成角的取值范围是____.
所成角的取值范围是____.
【答案】![]()
【解析】
先由题意,取![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得到
,得到![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,或所成角的补角,记异面直线
所成角,或所成角的补角,记异面直线![]() 与
与![]() 所成角为
所成角为![]() ,则
,则![]() ,根据题意,画出图形,结合翻折过程求出临界值,再由余弦定理,即可求出结果.
,根据题意,画出图形,结合翻折过程求出临界值,再由余弦定理,即可求出结果.
由题意,取![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
将![]() 沿
沿![]() 折起,在翻折过程中,始终有
折起,在翻折过程中,始终有![]() ,
,![]() ;
;
所以![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,或所成角的补角,
所成角,或所成角的补角,
记异面直线![]() 与
与![]() 所成角为
所成角为![]() ,则
,则![]()
因为![]() ,不放设
,不放设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
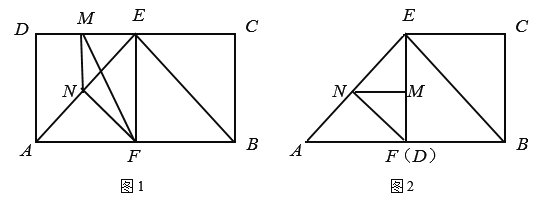
由题意可得,在翻折过程中,![]() 逐渐减小,当
逐渐减小,当![]() 点与
点与![]() 重合时,
重合时,![]() 最小,如图2;
最小,如图2;
此时![]() ;
;
翻折前,![]() 取最大,如图1;此时
取最大,如图1;此时![]() ,
,
所以![]() ,
,
由余弦定理可得:![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即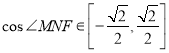 ,
,
所以 ,因此
,因此![]() ;
;
又翻折前,以及点![]() 点与
点与![]() 重合,这两种情况下,
重合,这两种情况下,![]() 与
与![]() 是相交直线,
是相交直线,
所以![]() ,即
,即![]() ;
;
故![]() .
.
故答案为:![]() .
.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
【题目】小王、小李在两次数学考试中答对题数如下表表示:
题型 答对 题数 姓名 | 期中考试 | 期末考试 | ||||
填空题 (每题3分) | 选择题 每题3分) | 解答题 (每题8分) | 填空题 (每题3分) | 选择题 每题3分) | 解答题 (每题8分) | |
小王 | 10 | 3 | 2 | 11 | 4 | 4 |
小李 | 9 | 5 | 3 | 7 | 3 | 3 |
(1)用矩阵表示小王和小李期中考试答对题数、期末考试答对题数、每种题型的分值;
(2)用矩阵运算表示他们在两次考试中各题型答对题总数;
(3)用矩阵计算小王、小李两次考试各题型平均答对题数;
(4)用矩阵计算他们期中、期末的成绩;
(5)如果期中考试成绩占40%,期末考试成绩占60%,用矩阵求两同学的总评成绩.
