题目内容
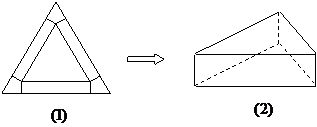
设底面为正三角形的直棱柱的体积为V,那么其表面最小时,底面边长为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析:设底面边长为x,侧棱长为l,则V=![]() x2·sin60°·l,
x2·sin60°·l,
∴l=![]()
∴S表=2S底+3S侧=x2sin60°+3xl=![]()
令S′表=![]()
∴x3=4V,即x=![]()
又当x∈(0,![]() )时,S′表<0,x∈(
)时,S′表<0,x∈(![]() ,V)时,S′表>0,
,V)时,S′表>0,
∴当x=![]() 时,表面积最小.
时,表面积最小.
答案:C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
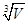 B.
B.
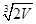 C.
C. 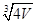 D. 2
D. 2