题目内容
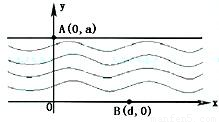
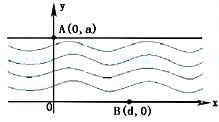 如图,在直线y=0和y=a(a>0)之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往.家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读.每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d,0)处的学校.已知船速为υ0(υ0>0),车速为2υ0(水流速度忽略不计).
如图,在直线y=0和y=a(a>0)之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往.家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读.每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d,0)处的学校.已知船速为υ0(υ0>0),车速为2υ0(水流速度忽略不计).(Ⅰ)若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间;
(Ⅱ)若d=
| a | 2 |
分析:(I)设该学生从家出发,先乘船渡河到达公路上某一点P(x,0)(0≤x≤d),再乘公交车去学校,所用的时间为t,则t=f(x)=
+
(0≤x≤d),求导函数,从而确定极值点,由此可求得函数的最值,从而得结论;
(II)由(I)的讨论可知,当d=
时,t=f(x)为(0,
]上的减函数,所以当x=
时,即该学生直接乘船渡河到达公路上学校,所用的时间最短,故可得结论.
| ||
| υ0 |
| d-x |
| 2υ0 |
(II)由(I)的讨论可知,当d=
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
解答:解:(I)设该学生从家出发,先乘船渡河到达公路上某一点P(x,0)(0≤x≤d),再乘公交车去学校,所用的时间为t,则t=f(x)=
+
(0≤x≤d).…(3分)
令f′(x)=0,得x=
a.…(5分)
且当0≤x<
a时,f′(x)<0,…(6分)
当
a<x≤d时,f′(x)>0,…(7分)
当x=
a时,所用的时间最短,最短时间为:t=
+
=(1+
)
.…(9分)
答:当d=2a时,该学生从家出发到达学校所用的最短时间是(1+
)
.
(II)由(I)的讨论可知,当d=
时,t=f(x)为(0,
]上的减函数,所以当x=
时,
即该学生直接乘船渡河到达公路上学校,所用的时间最短.…(12分)
最短的时间为t=
=
…(14分)
答:当d=
时,该学生从家出发到达学校所用的最短时间是
| ||
| υ0 |
| d-x |
| 2υ0 |
令f′(x)=0,得x=
| ||
| 3 |
且当0≤x<
| ||
| 3 |
当
| ||
| 3 |
当x=
| ||
| 3 |
| ||||||
| υ0 |
d-
| ||||
| 2υ0 |
| ||
| 2 |
| a |
| υ0 |
答:当d=2a时,该学生从家出发到达学校所用的最短时间是(1+
| ||
| 2 |
| a |
| υ0 |
(II)由(I)的讨论可知,当d=
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
即该学生直接乘船渡河到达公路上学校,所用的时间最短.…(12分)
最短的时间为t=
| ||||
| υ0 |
| ||
| 2υ0 |
答:当d=
| a |
| 2 |
| ||
| 2υ0 |
点评:本题以实际问题为载体,考查函数模型的构建,考查利用导数解决函数的最值,解题的关键是函数模型的构建.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 (2011•自贡三模)给出下列5个命题:
(2011•自贡三模)给出下列5个命题: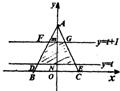 如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象.
如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象. ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间.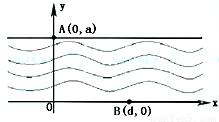
 ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间.