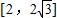题目内容

若y=3|x|（x∈[a，b]）的值域为[1，9]，则a2+b2-2a的取值范围是（　　）
A、[2，4]
B、[4，6]
C、[2，2
3
]
D、[4，12]
分析：先在坐标系中作出函数y=3|x|的图象，由图象和题意求出a、b的范围，再分别代入式子a2+b2-2a进行化简，并且结合它们的范围求出式子a2+b2-2a的取值范围．
解答：精英家教网解：在坐标系中作出函数y=3|x|的图象，
∵y=3|x|（x∈[a，b]）的值域为[1，9]，
∴由图得，函数的最小值是f（0）=1，最大值应是f（a）或f（b），
∵a＜b，∴由两种情况：a=-2，0≤b≤2或b=2，-2≤a≤0，
当a=-2，0≤b≤2时，设d=a2+b2-2a=8+b2，∵0≤b≤2，∴0≤b2≤4，
∴8≤d≤12，
当b=2，-2≤a≤0时，d=a2+b2-2a=3+（a-1）2
∵-2≤a≤0，∴1≤（a-1）2≤9，
∴4≤d≤12；
综上得，a2+b2-2a的取值范围是[4，12]．
故选D．
点评：本题考查了指数函数的图象以及性质，即根据指数函数的图象作出题中函数的图象，由图和函数的值域求取定义域，在求出所求式子的取值范围，考查了数形结合思想．
练习册系列答案
相关题目
对于定义在D上的函数y=f（x），若同时满足．
①存在闭区间[a，b]⊆D，使得任取x1∈[a，b]，都有f（x1）=c （c是常数）；
②对于D内任意x2，当x2∉[a，b]时总有f（x2）＞c称f（x）为“平底型”函数．
（1）（理）判断f1（x）=|x-1|+|x-2|，f2（x）=x+|x-2|是否是“平底型”函数？简要说明理由；
（文）判断f1（x）=|x-1|+|x-2|，f2（x）=x-|x-3|是否是“平底型”函数？简要说明理由；
（2）（理）设f（x）是（1）中的“平底型”函数，若|t-k|+|t+k|≥|k|•f（x），k∈R且k≠0，对一切t∈R恒成立，求实数x的范围；
（文）设f（x）是（1）中的“平底型”函数，若|t-1|+|t+1|≥f（x），对一切t∈R恒成立，求实数x的范围；
（3）（理）若F（x）=mx+
x2+2x+n
，x∈[-2，+∞）是“平底型”函数，求m和n的值；
（文）若F（x）=m|x-1|+n|x-2|是“平底型”函数，求m和n满足的条件．
定义：若{y|y=f（x），x∈A}=A，则f（x）称为A上的一阶回归函数；
若{y|y=f（f（x）），x∈A}=A，则f（x）称为A上的二阶回归函数；
若{y|y=f（f（f（x））），x∈A}=A，则f（x）称为A上的三阶回归函数．
下列判断正确的个数是（　　）
①f（x）=3-x是[1，2]上的一阶回归函数；
②f(x)=1-(
1
2
)x是[-1，0]上的一阶回归函数
③f(x)=
-2
x
是（0，+∞）上的二阶回归函数；
④f(x)=
1
1-x
是（2，+∞）上的三阶回归函数．
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）将函数y=f（x）图象向右平移一个单位即可得到函数y=φ（x）的图象，试写出y=φ（x）的解析式及值域；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
若y=3|x|（x∈[a，b]）的值域为[1，9]，则a2+b2-2a的取值范围是（ ）
A．[2，4]
B．[4，6]
C．
D．[4，12]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网