题目内容
11.若不等式x2-logmx<0在(0,$\frac{1}{3}$)内恒成立,求实数m的取值范围.分析 作出y=x2和y=logmx的草图,利用数学结合得出0<m<1,只要x=$\frac{1}{3}$时,y=logm$\frac{1}{3}$≥$\frac{1}{9}$=logm${m}^{\frac{1}{9}}$,进而求出m的范围.
解答 解:由x2-logmx<0,得x2<logmx,在同一坐标系中作y=x2和y=logmx的草图,如图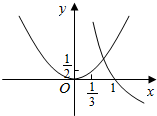
要使由x2<logmx在(0,$\frac{1}{3}$)内恒成立,只要y=logmx在(0,$\frac{1}{3}$)内的图象在y=x2的上方,于是0<m<1;
∵x=$\frac{1}{3}$时,y=x2=$\frac{1}{9}$,
∴只要x=$\frac{1}{3}$时,y=logm$\frac{1}{3}$≥$\frac{1}{9}$=logm${m}^{\frac{1}{9}}$,
∴$\frac{1}{3}$≤${m}^{\frac{1}{9}}$,即m≥($\frac{1}{3}$)9,
又0<m<1
∴1>m≥($\frac{1}{3}$)9
即实数m的取值范围是1>m≥($\frac{1}{3}$)9.
点评 考查了函数作图,利用数学结合的思想分析问题.数学结合的思想的利用.

练习册系列答案
相关题目
1.△ABC中,a,b、c分别为∠A、∠B、∠C的对边,如果a、b、c成等差数列,∠B=60°,△ABC的面积为$\frac{{3\sqrt{3}}}{2}$,那么b等于( )
| A. | $\sqrt{6}$ | B. | 4 | C. | $\sqrt{5}$ | D. | $2\sqrt{3}$ |