题目内容
2.已知二次函数f(x)=px2+qx.满足f(x-1)=f(x)+x-1.(1)求f(x)的解析式;
(2)求f(x)<0时.X的取值集合;
(3)设a为常数,F(x)=|f(x)|-a,试讨论方程F(x)=0的解的个数.
分析 (1)根据f(x-1)=f(x)+x-1,结合多项式相等的充要条件,求出p,q的值,可得f(x)的解析式;
(2)根据二次函数的图象和性质,求出满足f(x)<0的x的取值范围,可得答案;
(3)程F(x)=0的解的个数,即函数y=|f(x)|与直线y=a的交点的个数,画出函数y=|f(x)|的图象,数形结合,可得答案.
解答 解:(1)∵二次函数f(x)=px2+qx.满足f(x-1)=f(x)+x-1,
∴p(x-1)2+q(x-1)=px2+qx+x-1,
∴(2p+1)x+q-p-1=0,
∴$\left\{\begin{array}{l}2p+1=0\\ q-p-1=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}q=\frac{1}{2}\\ p=-\frac{1}{2}\end{array}\right.$,
∴f(x)=$-\frac{1}{2}$x2+$\frac{1}{2}$x;
(2)解f(x)=$-\frac{1}{2}$x2+$\frac{1}{2}$x<0得:
x∈(-∞,0)∪(1,+∞),
(3)方程F(x)=0的解的个数,即函数y=|f(x)|与直线y=a的交点的个数,
函数y=|f(x)|的图象如下图所示: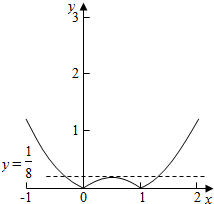
由图可得:
当a<0时,函数y=|f(x)|的图象与直线y=a无交点,此时方程F(x)=0无解;
当a=0,或a$>\frac{1}{8}$时,函数y=|f(x)|的图象与直线y=a有两个交点,此时方程F(x)=0有两个解;
当a=$\frac{1}{8}$时,函数y=|f(x)|的图象与直线y=a有三个交点,此时方程F(x)=0有三个解;
当0<a<$\frac{1}{8}$时,函数y=|f(x)|的图象与直线y=a有四个交点,此时方程F(x)=0有四个解;
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | c<b<a |
| A. |  [-2,+∞) | B. |  (-∞,2) | C. |  (-1,2) | D. |  [-1,+∞) |
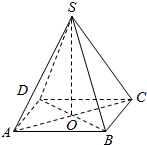 如图,四棱锥S-ABCD的侧倰均相等,底面ABCD为平行四边形,其对角线交点为O.
如图,四棱锥S-ABCD的侧倰均相等,底面ABCD为平行四边形,其对角线交点为O.