题目内容
已知函数f(x)=ax2﹣4x+c(a,c∈R),满足f(2)=9,f(c)<a,且函数f(x)的值域为[0,+∞).
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设函数g(x)= (k∈R),对任意x∈[1,2],存在x0∈[﹣1,1],使得g(x)<f(x0)求k的取值范围.
(k∈R),对任意x∈[1,2],存在x0∈[﹣1,1],使得g(x)<f(x0)求k的取值范围.
解:(Ⅰ)根据f(2)=9,得4a+c=17
由函数f(x)的值域为[0,+∞)知,方程ax2-4x+c=0,判别式△=0,即 ac=4,
又f(c)<a,∴ac2-4c+c<a,即c<a,
解得:a=4,c=1,所以f(x)=4x2-4x+1.
(Ⅱ)当x∈[-1,1]时,f(x)∈[0,9],
对任意x∈[1,2],存在x0∈[-1,1],使得g(x)<f(x0),即
g(x)= <9,即4x2+(k-13)x-2<0对任意x∈[1,2]恒成立.
<9,即4x2+(k-13)x-2<0对任意x∈[1,2]恒成立.
设h(x)=4x2+(k-13)x-2,则
 即
即
∴k的取值范围是(-∞,6).

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案某同学在研究性学习中,收集到某制药厂车间工人数(单位:十人)与药品产量(单位:万盒)的数据如表所示:
| 工人数:x(单位:十人) | 1 | 2 | 3 | 4 |
| 药品产量:y(单位:万盒) | 3 | 4 | 5 | 6 |
(1)请画出如表数据的散点图;
(2)参考公式,根据表格提供的数据,用最小二乘法求出y关于x的线性回归方程y=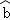 x+
x+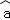 ;(参考数据
;(参考数据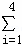 i2=30,
i2=30,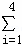 xiyi=50)
xiyi=50)
(3)试根据(2)求出的线性回归方程,预测该制药厂车间工人数为45时,药品产量是多少?
设等差数列{an}的前n项和Sn,若S15>0,S16<0,则数列{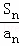 }的前15项中最大的项是( )
}的前15项中最大的项是( )
|
| A. | 第1项 | B. | 第8项 | C. | 第9项 | D. | 第15项 |
圆(x﹣3)2+y2=4与圆x2+(y﹣4)2=16的位置关系为( )
|
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 相离 |
在平面直角坐标系中,定义d(P,Q)=|x1﹣x2|+|y1﹣y2|为两点P(x1,y1),Q(x2,y2)之间的“折线距离”,在这个定义下,给出下列命题:
①到原点的“折线距离”等于1的点的集合是一个圆;
②到原点的“折线距离”小于等于2的点构成的区域面积为8;
③到M(0,﹣2),N(0,2)两点的“折线距离”相等的点的轨迹方程是y=0;
④直线y=x+1上的点到N(0,2)的“折线距离”的最小值为1.
其中真命题有( )
|
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
演绎推理“因为对数函数y=logax(a>0且a≠1)是增函数,而函数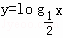 是对数函数,所以
是对数函数,所以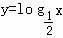 是增函数”所得结论错误的原因是( )
是增函数”所得结论错误的原因是( )
|
| A. | 大前提错误 | B. | 小前提错误 |
|
| C. | 推理形式错误 | D. | 大前提和小前提都错误 |
某款手机的广告宣传费用x(单位万元)与利润y(单位万元)的统计数据如下表:
| 广告宣传费用x | 6 | 5 | 7 | 8 |
| 利润y | 34 | 26 | 38 | 42 |
根据上表可得线性回归方程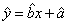 中的
中的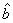 为9.4,据此模型预报广告宣传费用为10万元时利润为
为9.4,据此模型预报广告宣传费用为10万元时利润为
A.65.0万元 B.67.9万元 C.68.1万元 D.68.9万元
 R
R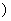 ,则下列四个结论:
,则下列四个结论: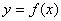 的最小值为
的最小值为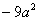 .
.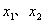 ,都有
,都有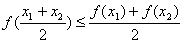 .
.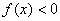 的解集是
的解集是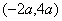 .
. 恒成立,则实数
恒成立,则实数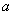 能取的最大整数是
能取的最大整数是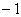 .
.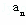 ﹣1}的前n项和Sn.
﹣1}的前n项和Sn.