题目内容
椭圆C:
+
=1的左、右顶点分别为A1,A2,点P在C上且直线PA2的斜率的取值范围是[-2,-1],那么直线PA1斜率的取值范围是 .
| x2 |
| 4 |
| y2 |
| 2 |
分析:由椭圆C:
+
=1可知其左顶点A1(-2,0),右顶点A2(2,0).设P(x0,y0)(x0≠±2),代入椭圆方程可得
=-
.利用斜率计算公式可得kPA1•kPA2,再利用已知给出的kPA1的范围即可解出.
| x2 |
| 4 |
| y2 |
| 2 |
| y02 |
| x02-4 |
| 3 |
| 4 |
解答:解:由椭圆C:
+
=1可知其左顶点A1(-2,0),右顶点A2(2,0).
设P(x0,y0)(x0≠±2),则
+
=1⇒
=-
,
∵KPA1•KPA2=
•
=-
,
KPA2∈[-2,-1],
∴-2≤-
≤-1.
解答
≤KPA1≤
.
故答案是[
,
].
| x2 |
| 4 |
| y2 |
| 2 |
设P(x0,y0)(x0≠±2),则
| x02 |
| 4 |
| y02 |
| 2 |
| y02 |
| x02-4 |
| 1 |
| 2 |
∵KPA1•KPA2=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
| 1 |
| 2 |
KPA2∈[-2,-1],
∴-2≤-
| 1 |
| 2KPA1 |
解答
| 1 |
| 4 |
| 1 |
| 2 |
故答案是[
| 1 |
| 4 |
| 1 |
| 2 |
点评:熟练掌握椭圆的标准方程及其性质、斜率的计算公式、不等式的性质等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
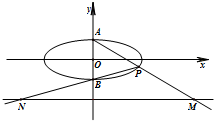 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: