题目内容
已知四边形ABCD的对角线互相平分且相等，PA⊥面ABCD，则下列等式中不一定成立的是（ ）A．
•
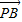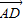=0B．
•
=0C．
•
=0D．
•
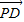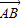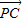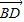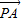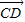=0
【答案】分析：利用线面垂直的判定与性质、垂直与数量积的关系等即可得出．
解答：解：如图所示，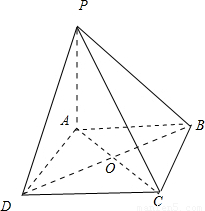
∵四边形ABCD的对角线互相平分且相等，∴四边形ABCD是正方形．
∴AD⊥AB，AC⊥BD．
∵PA⊥面ABCD，∴PA⊥AD，PA⊥CD，∴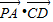
=0，故D正确．
又PA∩PB=P，∴AD⊥平面PAB．∴AD⊥PB，∴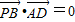
，故A正确．
同理AB⊥PD，∴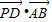
=0．
综上可知：A，B，D都正确．
因此只有C不一定成立．
故选C．
点评：熟练掌握线面垂直的判定与性质、垂直与数量积的关系等是解题的关键．
解答：解：如图所示，
∵四边形ABCD的对角线互相平分且相等，∴四边形ABCD是正方形．
∴AD⊥AB，AC⊥BD．
∵PA⊥面ABCD，∴PA⊥AD，PA⊥CD，∴
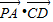=0，故D正确．又PA∩PB=P，∴AD⊥平面PAB．∴AD⊥PB，∴
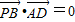，故A正确．同理AB⊥PD，∴
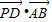=0．综上可知：A，B，D都正确．
因此只有C不一定成立．
故选C．
点评：熟练掌握线面垂直的判定与性质、垂直与数量积的关系等是解题的关键．
练习册系列答案
相关题目
已知四边形ABCD的三个顶点A（0，2），B（-1，-2），C（3，1），且
=2
，则顶点D的坐标为（ ）
| BC |
| AD |
A、(2，
| ||
B、(2，-
| ||
| C、（3，2） | ||
| D、（1，3） |
（1）自圆O外一点P引切线与圆切于点A，M为PA中点，过M引割线交圆于B，C两点．求证：∠MCP=∠MPB．