题目内容
(本小题满分12分)
椭圆C的中心为坐标原点O,焦点在y轴上,短轴长为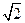 、离心率为
、离心率为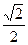 ,直线
,直线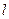 与y轴交于点P(0,
与y轴交于点P(0,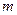 ),与
),与 椭圆C交于相异两点A、B,且
椭圆C交于相异两点A、B,且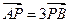 。
。
(I)求椭圆方程;
(II)求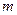 的取值范围。
的取值范围。
椭圆C的中心为坐标原点O,焦点在y轴上,短轴长为
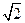 、离心率为
、离心率为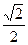 ,直线
,直线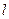 与y轴交于点P(0,
与y轴交于点P(0,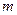 ),与
),与 椭圆C交于相异两点A、B,且
椭圆C交于相异两点A、B,且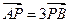 。
。(I)求椭圆方程;
(II)求
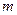 的取值范围。
的取值范围。解:(I)设C: 设
设
由条件知 ,
, ,∴
,∴
 …3分
…3分
故C的方程为: …………5分
…………5分
(II)设 与椭圆C交点为A(
与椭圆C交点为A( ),B(
),B( )
)
由 得
得
得(k2+2)x2+2kmx+(m2-1)=0
 (*)
(*)
 …………8分
…………8分
∵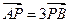 ∴
∴ ∴
∴
消去 ,得
,得 ,∴
,∴
整理得
 …………10分
…………10分
 时,上式不成立;
时,上式不成立;  时,
时, ,
,
由(*)式得
因 ∴
∴ ,∴
,∴ 或
或
即所求 的取值范围为
的取值范围为 …………13分
…………13分
 设
设
由条件知
 ,
, ,∴
,∴
 …3分
…3分故C的方程为:
 …………5分
…………5分(II)设
 与椭圆C交点为A(
与椭圆C交点为A( ),B(
),B( )
)
由
 得
得
得(k2+2)x2+2kmx+(m2-1)=0
 (*)
(*) …………8分
…………8分∵
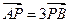 ∴
∴ ∴
∴
消去
 ,得
,得 ,∴
,∴
整理得

 …………10分
…………10分 时,上式不成立;
时,上式不成立;  时,
时, ,
,由(*)式得

因
 ∴
∴ ,∴
,∴ 或
或
即所求
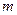 的取值范围为
的取值范围为 …………13分
…………13分略

练习册系列答案
相关题目
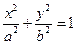 (a>b>0)的离心率
(a>b>0)的离心率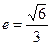 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为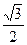 .
.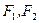 是椭圆
是椭圆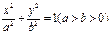 的两个焦点,
的两个焦点,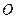 为坐标原点,点
为坐标原点,点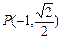 在椭圆上,且
在椭圆上,且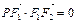 ,⊙
,⊙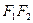 为直径的圆,直线
为直径的圆,直线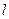 :
: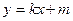 与⊙
与⊙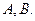
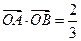 ,求
,求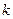 的值.
的值.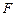 是椭圆
是椭圆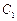 :
: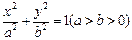 的右焦点,也是抛物线
的右焦点,也是抛物线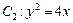 的焦点,点P为
的焦点,点P为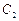 在第一象限的交点,且
在第一象限的交点,且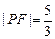 .
.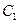 的方程;
的方程;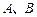 ,过
,过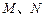 两点,记
两点,记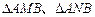 的面积分别为
的面积分别为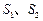 ,求
,求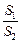 的取值范围。
的取值范围。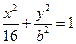
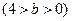 ,
,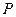 为椭圆上的动点,
为椭圆上的动点,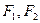 为椭圆的两焦点,当
为椭圆的两焦点,当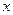 轴上时,过
轴上时,过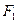 作
作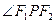 的外角平分线的垂线
的外角平分线的垂线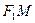 ,垂足为
,垂足为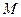 ,当点
,当点
 的方程;
的方程; 、
、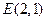 ,试探究是否存在这样的点
,试探究是否存在这样的点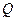 :点
:点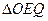 的面积
的面积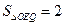 ?若存
?若存 在,求出点
在,求出点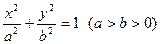 的焦点F1,F2,短轴长为8,离心率为
的焦点F1,F2,短轴长为8,离心率为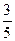 ,过F1的直线交椭圆于A、B两点,则
,过F1的直线交椭圆于A、B两点,则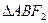 的周长为( )
的周长为( ) D、40
D、40
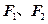 为中心在原点焦点在
为中心在原点焦点在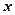 的椭圆
的椭圆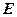 的左、右焦点,抛物线
的左、右焦点,抛物线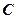 以
以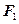 为顶点,
为顶点,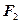 为焦点,设
为焦点,设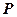 为椭圆与抛物线的一个交点,如果椭圆的离心率为
为椭圆与抛物线的一个交点,如果椭圆的离心率为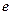 ,且
,且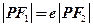 ,则
,则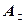
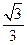
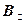
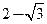

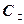
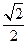
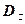
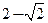
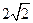 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线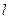 与x轴相交于点A,
与x轴相交于点A,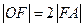 ,过点A的直线与椭圆相交于P,Q两点,
,过点A的直线与椭圆相交于P,Q两点,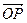 ·
·
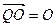 ,求直线PQ的方
,求直线PQ的方 程。
程。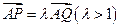 ,过点P且平行于准线l的直线与椭圆相交于另一点M,证明
,过点P且平行于准线l的直线与椭圆相交于另一点M,证明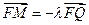
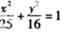 上一点P到其左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到其左准线的距离为10,F是该椭圆的左焦点,若点M满足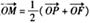 (其中O为坐标原点),则
(其中O为坐标原点),则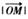 =_________
=_________