题目内容
设函数
.（Ⅰ）求
的单调区间和极值；
（Ⅱ）若对一切
，
，求
的最大值.
解答：（Ⅰ），
当时，；当时，；
故
在
单调增加，在
单调减少.
的极小值
，极大值
.
（Ⅱ）由
知
，
即
，由此及（Ⅰ）知
的最小值为
，最大值为
.
因此对一切
，
的充要条件是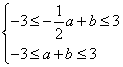
，
即
，
满足约束条件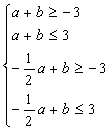
，由线性规划得，
的最大值为5.
练习册系列答案
相关题目
.题目内容
设函数.（Ⅰ）求的单调区间和极值；
（Ⅱ）若对一切，，求的最大值.
解答：（Ⅰ），
当时，；当时，；
故在单调增加，在单调减少.
的极小值，极大值.
（Ⅱ）由知，
即，由此及（Ⅰ）知的最小值为，最大值为.
因此对一切，的充要条件是，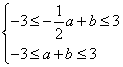
即，满足约束条件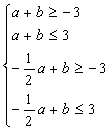，由线性规划得，的最大值为5.
.
，求
的最小值；
，讨论函数
，
的反函数
；
，当
，
时，
，求
的取值范围．
，（1）求
的振幅，周期和初相；（2）求
值组成的集合。（3）求
.
，求
的最小值；
，讨论函数