题目内容
已知△ABC的三内角A、B、C满足A+C=2B,设x=cos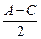 ,f(x)=cosB(
,f(x)=cosB(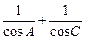 ).
).
(1)试求函数f(x)的解析式及其定义域;
(2)判断其单调性,并加以证明;
(3)求这个函数的值域.
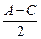 ,f(x)=cosB(
,f(x)=cosB(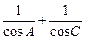 ).
).(1)试求函数f(x)的解析式及其定义域;
(2)判断其单调性,并加以证明;
(3)求这个函数的值域.
(1)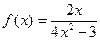 ,定义域为(
,定义域为( ,
, )∪(
)∪( ,1] (2) f(x)在(
,1] (2) f(x)在(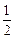 ,
,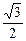 )和(
)和(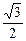 ,1
,1 上都是减函数,(3) f(x)的值域为(-∞,-
上都是减函数,(3) f(x)的值域为(-∞,-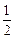 )∪[2,+∞
)∪[2,+∞
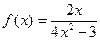 ,定义域为(
,定义域为( ,
, )∪(
)∪( ,1] (2) f(x)在(
,1] (2) f(x)在(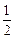 ,
,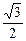 )和(
)和(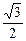 ,1
,1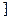 上都是减函数,(3) f(x)的值域为(-∞,-
上都是减函数,(3) f(x)的值域为(-∞,-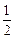 )∪[2,+∞
)∪[2,+∞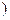
(1)∵A+C=2B,∴B=60°,A+C=120°
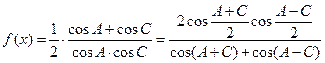
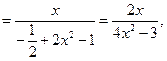
∵0°≤|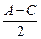 |<60°,∴x=cos
|<60°,∴x=cos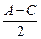 ∈(
∈( ,1
,1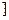
又4x2-3≠0,∴x≠ ,∴定义域为(
,∴定义域为( ,
, )∪(
)∪( ,1].
,1].
(2)设x1<x2,
∴f(x2)-f(x1)=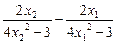 =
=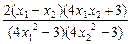 ,
,
若x1,x2∈(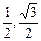 ),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0
),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0
即f(x2)<f(x1),若x1,x2∈( ,1],则4x12-3>0.
,1],则4x12-3>0.
4x22-3>0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0.
即f(x2)<f(x1),∴f(x)在( ,
, )和(
)和( ,1
,1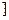 上都是减函数.
上都是减函数.
(3)由(2)知,f(x)<f( )=-
)=- 或f(x)≥f(1)=2.
或f(x)≥f(1)=2.
故f(x)的值域为(-∞,- )∪[2,+∞
)∪[2,+∞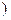 .
.
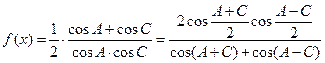
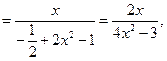
∵0°≤|
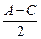 |<60°,∴x=cos
|<60°,∴x=cos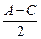 ∈(
∈( ,1
,1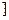
又4x2-3≠0,∴x≠
 ,∴定义域为(
,∴定义域为( ,
, )∪(
)∪( ,1].
,1]. (2)设x1<x2,
∴f(x2)-f(x1)=
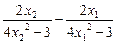 =
=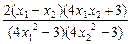 ,
,若x1,x2∈(
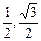 ),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0
),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0即f(x2)<f(x1),若x1,x2∈(
 ,1],则4x12-3>0.
,1],则4x12-3>0.4x22-3>0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0.
即f(x2)<f(x1),∴f(x)在(
 ,
, )和(
)和( ,1
,1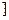 上都是减函数.
上都是减函数.(3)由(2)知,f(x)<f(
 )=-
)=- 或f(x)≥f(1)=2.
或f(x)≥f(1)=2.故f(x)的值域为(-∞,-
 )∪[2,+∞
)∪[2,+∞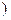 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
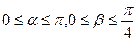 ,且
,且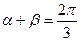 .
.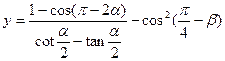 的最大值,并求出相应的
的最大值,并求出相应的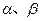 的值.
的值.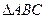 中,角
中,角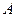 、
、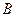 、
、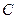 的对边分别为
的对边分别为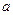 、
、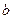 、
、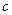 ,且
,且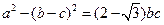 ,
,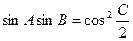 ,
,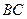 边上中线
边上中线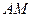 的长为
的长为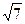 .
.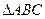 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为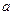 、
、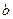 、
、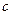 ,已知
,已知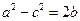 ,且
,且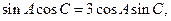 求b
求b 

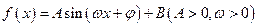 的一系列对应值如下表:
的一系列对应值如下表: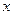
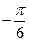
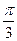
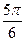
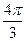
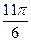
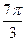
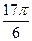
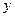
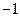
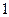
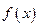 的一个解析式;
的一个解析式;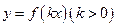 周期为
周期为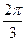 ,当
,当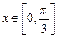 时,方程
时,方程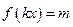 恰有两个不同的解,求实数
恰有两个不同的解,求实数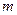 的取值范围;
的取值范围;
 的最大值及最小正周期;
的最大值及最小正周期; 的x的取值范围。
的x的取值范围。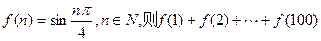 =____________.
=____________.