题目内容
(本题满分16分)
已知函数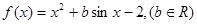 ,且对任意
,且对任意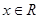 ,有
,有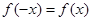 .
.
(1)求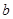 ;
;
(2)已知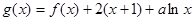 在区间(0,1)上为单调函数,求实数
在区间(0,1)上为单调函数,求实数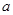 的取值范围.
的取值范围.
(3)讨论函数 的零点个数?(提示:
的零点个数?(提示: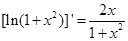 )
)
【答案】
解:(1)由
得 ………………2分
………………2分
(2)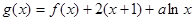

所以 ………………4分
………………4分
依题意,
或 在(0,1)上恒成立………………6分
在(0,1)上恒成立………………6分
即
或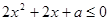 在(0,1)上恒成立
在(0,1)上恒成立
由 在(0,1)上恒成立,
在(0,1)上恒成立,
可知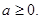
由 在(0,1)上恒成立,
在(0,1)上恒成立,
可知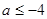 ,所以
,所以 或
或 ………………9分
………………9分
(3) ,
,
令
所以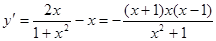 ………………10分
………………10分
令 ,则
,则 ,列表如下:
,列表如下:
|
|
(-∞,-1) |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1,+∞) |
|
|
+ |
0 |
— |
0 |
+ |
0 |
— |
|
h(x) |
单调递增 |
极大值 |
单调递减 |
极小值1 |
单调递增 |
极大值 |
单调递减 |
所以当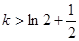 时,函数无零点;
时,函数无零点;
当 1或
1或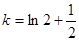 时,函数有两个零点;
时,函数有两个零点;
当 时,函数有三个零点。
时,函数有三个零点。
当 时,函数有四个零点。………………16分
时,函数有四个零点。………………16分
【解析】略

练习册系列答案
相关题目





 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在