题目内容
9．已知复数$z=\frac{1+3i}{3-i}$，$\overline z$是z的共轭复数，则$\overline z$•z=（ ）| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 1 | D． | -1 |
分析 把复数z的分子提取i，约分后化简z，代入$\overline z$•z得答案．
解答 解：∵$z=\frac{1+3i}{3-i}=\frac{（3-i）i}{3-i}=i$，
∴$z•\overline z=i•（-i）=1$．
故选：C．
点评 本题考查复数代数形式的乘除运算，是基础的计算题．
练习册系列答案
相关题目
20．
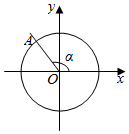如图所示，在平面直角坐标系xOy中，角α的终边与单位圆交于点A．若点A的纵坐标是$\frac{4}{5}$，那么sinα的值是（ ）
如图所示，在平面直角坐标系xOy中，角α的终边与单位圆交于点A．若点A的纵坐标是$\frac{4}{5}$，那么sinα的值是（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
17．从点P（-2，1）向圆x2+y2-2x-2my+m2=0作切线，当切线长最短时，m的值为（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
1．与sin2016°最接近的数是（ ）
| A． | $\frac{11}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -1 |