题目内容
已知f（x）=-4cos2x+4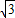
asinxcosx，将f（x）的图象按向量
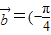，2）平移后，图象关于直线x=
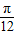对称．（1）求实数a的值，并求f（x）取得最大值时x的集合；
（2）求f（x）的单调递增区间．
【答案】分析：（1）求得将f（x）的图象按向量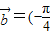
，2）平移后的解析式为g（x）=f（x+
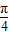）+2=2sin2x+2
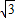acos2x，利用其图象关于直线x=
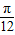对称可求得a；
（2）将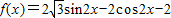
化为
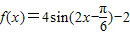，利用正弦函数的单调性可求得f（x）的单调递增区间．
解答：解：（1）f（x）=2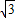
asin2x-2cos2x-2，
将f（x）的图象按向量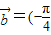
，2）平移后的解析式为g（x）=f（x+
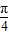）+2=2sin2x+2
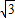acos2x．…（3分）
∵g（x）的图象关于直线x=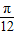
对称，
∴有g（0）=g（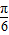
），即2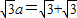
a，解得a=1． …（5分）
则f（x）=2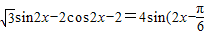
）-2． …（6分）
当2x-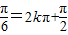
，即x=kπ+
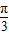时，f（x）取得最大值2．…（7分）
因此，f（x）取得最大值时x的集合是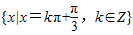
．…（8分）
（2）由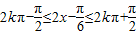
，解得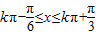
．
因此，f（x）的单调递增区间是[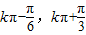
]（k∈Z）．…（12分）
点评：本题考查三角函数的最值，重点考查正弦函数的对称性质与单调性，难点是辅助角公式的理解与应用，属于中档题．
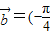，2）平移后的解析式为g（x）=f（x+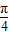）+2=2sin2x+2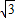acos2x，利用其图象关于直线x=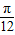对称可求得a；（2）将
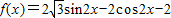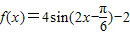化为，利用正弦函数的单调性可求得f（x）的单调递增区间．解答：解：（1）f（x）=2
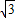asin2x-2cos2x-2，将f（x）的图象按向量
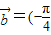，2）平移后的解析式为g（x）=f（x+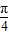）+2=2sin2x+2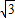acos2x．…（3分）∵g（x）的图象关于直线x=
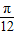对称，∴有g（0）=g（
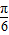），即2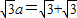a，解得a=1． …（5分）则f（x）=2
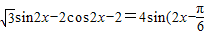）-2． …（6分）当2x-
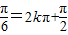，即x=kπ+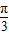时，f（x）取得最大值2．…（7分）因此，f（x）取得最大值时x的集合是
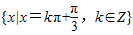．…（8分）（2）由
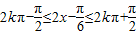，解得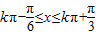．因此，f（x）的单调递增区间是[
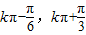]（k∈Z）．…（12分）点评：本题考查三角函数的最值，重点考查正弦函数的对称性质与单调性，难点是辅助角公式的理解与应用，属于中档题．
练习册系列答案
相关题目
已知f（x）为偶函数，且f （2+x）=f （2-x），当-2≤x≤0时，f（x）=2x，an=f （n），n∈N*，则a2010的值为（ ）
| A、2010 | ||
| B、4 | ||
C、
| ||
| D、-4 |