题目内容
已知抛物线C: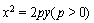 ,定点M(0,5),直线
,定点M(0,5),直线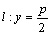 与
与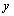 轴交于点F,O为原点,若以OM为直径的圆恰好过
轴交于点F,O为原点,若以OM为直径的圆恰好过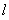 与抛物线C的交点.
与抛物线C的交点.
(1)求抛物线C的方程;
(2)过点M作直线交抛物线C于A,B两点,连AF,BF延长交抛物线分别于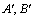 ,求证: 抛物线C分别过
,求证: 抛物线C分别过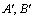 两点的切线的交点Q在一条定直线上运动.
两点的切线的交点Q在一条定直线上运动.
【答案】
(1)抛物线C的方程为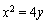 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)求抛物线C的方程,只需求出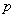 的值即可,由已知可知直线
的值即可,由已知可知直线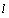 与
与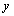 轴的交点
轴的交点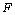 为抛物线C的焦点,又以
为抛物线C的焦点,又以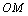 为直径的圆恰好过直线
为直径的圆恰好过直线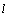 抛物线的交点,设交点为
抛物线的交点,设交点为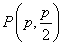 ,则
,则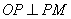 ,故
,故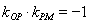 ,即
,即 ,解得
,解得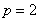 ,从而可得抛物线C的方程;(2),求证: 抛物线C分别过
,从而可得抛物线C的方程;(2),求证: 抛物线C分别过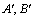 两点的切线的交点Q在一条定直线上运动,找出交点
两点的切线的交点Q在一条定直线上运动,找出交点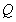 点的坐标即可,故需求出过
点的坐标即可,故需求出过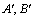 两点的切线的方程,而
两点的切线的方程,而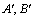 与
与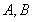 有关,故可设出直线AB的方程为
有关,故可设出直线AB的方程为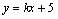 (斜率一定存在),再设出
(斜率一定存在),再设出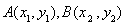 ,
,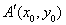 ,利用三点共线可得
,利用三点共线可得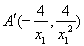 ,
,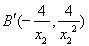 ,再由导数的几何意义,求出斜率,得过点
,再由导数的几何意义,求出斜率,得过点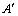 的切线方程为:
的切线方程为: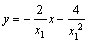 ,过点
,过点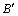 的切线方程为:
的切线方程为: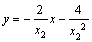 ,解出
,解出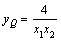 ,结合
,结合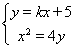 ,得
,得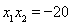 ,即得
,即得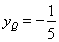 ,从而得证。
,从而得证。
试题解析:(1) 直线
直线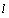 与
与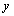 轴的交点
轴的交点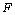 为抛物线C的焦点,又以
为抛物线C的焦点,又以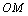 为直径的圆恰好过直线
为直径的圆恰好过直线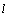 抛物线的交点,
抛物线的交点,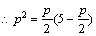 ,
,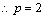
所以抛物线C的方程为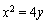
(2)由题意知直线AB的斜率一定存在,设直线AB的方程为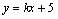 ,
,
又设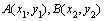 ,
,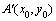
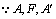 共线,
共线,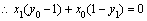 ,
,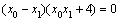
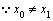
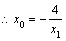 ,
,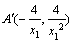 ,同理可求
,同理可求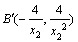
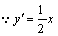 ,
, 过点
过点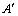 的切线的斜率为
的切线的斜率为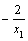 ,切线方程为:
,切线方程为: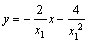 ,
,
同理得过点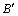 的切线方程为:
的切线方程为: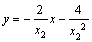 ,联立得:
,联立得: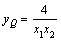
由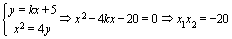
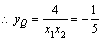 ,即点Q在定直线
,即点Q在定直线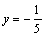 上运动.
上运动.
考点:抛物线方程,直线与抛物线的综合问题.

练习册系列答案
相关题目
 (2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.
(2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.