题目内容
已知e1、e2是两个不共线的向量,而a=k2 e1+(1-
解析:∵a与b共线,
∴存在实数λ使得a=λb即k2 e1+(1-![]() k)e2=λ(2e1+3e2)=2λe1+3λe2,即
k)e2=λ(2e1+3e2)=2λe1+3λe2,即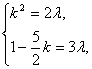
解得k=![]() 或-2.
或-2.
答案:![]() 或-2
或-2

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
题目内容
已知e1、e2是两个不共线的向量,而a=k2 e1+(1-
解析:∵a与b共线,
∴存在实数λ使得a=λb即k2 e1+(1-![]() k)e2=λ(2e1+3e2)=2λe1+3λe2,即
k)e2=λ(2e1+3e2)=2λe1+3λe2,即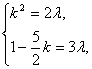
解得k=![]() 或-2.
或-2.
答案:![]() 或-2
或-2

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案