题目内容
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )
| A.2πR2 | B. πR2 πR2 |
C.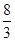 πR2 πR2 | D. πR2 πR2 |
B
解析试题分析:设内接圆柱的底面半径为 ,高为
,高为 ,全面积为
,全面积为 ,则有
,则有


 当
当 时,
时, 取最大值
取最大值
故答案为:
考点:实际问题中的最值问题.

练习册系列答案
相关题目
正六棱柱的底面边长为4,高为6,则它的外接球的表面积为( )
A. | B. | C. | D. |
一个几何体的三视图如图所示,则这个几何体的表面积等于( )
A. | B. | C. | D. |
某三棱锥的三视图如图所示,则该三棱锥的体积是( )
A. | B. | C. | D.1 |
有一个长方体容器 ,装的水恰好占其容积的一半;
,装的水恰好占其容积的一半; 表示水平的桌面,容器一边
表示水平的桌面,容器一边 紧贴桌面,沿
紧贴桌面,沿 将其翻转使之倾斜,最后水面(阴影部分)与其各侧棱的交点分别是
将其翻转使之倾斜,最后水面(阴影部分)与其各侧棱的交点分别是 (如图),设翻转后容器中的水形成的几何体是
(如图),设翻转后容器中的水形成的几何体是 ,翻转过程中水和容器接触面积为
,翻转过程中水和容器接触面积为 ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 是棱柱, 是棱柱, 逐渐增大 逐渐增大 |
B. 是棱柱, 是棱柱, 始终不变 始终不变 |
C. 是棱台, 是棱台, 逐渐增大 逐渐增大 |
D. 是棱台, 是棱台, 始终不变 始终不变 |
一个几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
| A.9 | B.10 | C.11 | D. |
一个几何体的三视图如图所示,其中府视图为正三角形,则侧视图的面积为( )
| A.8 | B. | C. | D.4 |




