Question

【题目】如图，现要在一块半径为1m，圆心角为 的扇形纸报AOB上剪出一个平行四边形MNPQ，使点P在弧AB上，点Q在OA上，点M、N在OB上，设∠BOP=θ，平行四边形MNPQ的面积为S．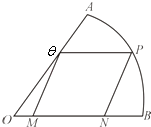
（1）求S关于θ的函数关系式；
（2）求S的最大值及相应的θ角．

Answer 1

【答案】
（1）解：分别过P、Q作PD⊥OB于D，QE⊥OB于E，则QEDP为矩形（2分）

由扇形半径为1cm，PD=sinθ，OD=cosθ

在Rt△OEQ中

MN=OD﹣OE=

=

（2）解：

，

当 时，

【解析】（1）分别过P、Q作PD⊥OB于D，QE⊥OB于E，则QEDP为矩形，求出边长即可求S关于θ的函数关系式；（2）利用二倍角公式、两角和的正弦函数化简函数的表达式为一个角的一个三角函数的形式，通过θ的范围求出S的最大值及相应的θ角．
【考点精析】根据题目的已知条件，利用三角函数的最值的相关知识可以得到问题的答案，需要掌握函数，当时，取得最小值为；当时，取得最大值为，则，，．