题目内容
已知函数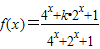 .
.(1)若对于任意的x∈R,f(x)>0恒成立,求实数k的取值范围;
(2)若f(x)的最小值为-2,求实数k的值;
(3)若对任意的x1,x2,x3∈R,均存在以f(x1),f(x2),f(x3)为三边长的三角形,求实数k的取值范围.
【答案】分析:(1)问题等价于4x+k•2x+1>0恒成立,分离出参数k后转化为求函数的最值问题即可;
(2) ,令
,令 ,则
,则 ,分k>1,k=1,k<1三种情况进行讨论求出f(x)的最小值,令其为-2即可解得k值;
,分k>1,k=1,k<1三种情况进行讨论求出f(x)的最小值,令其为-2即可解得k值;
(3)由题意,f(x1)+f(x2)>f(x3)对任意x1,x2,x3∈R恒成立.当k=1时易判断;当k>1,k<1时转化为函数的最值问题解决即可,借助(2)问结论易求函数的最值;
解答:解:(1)因为4x+2x+1>0,所以f(x)>0恒成立,等价于4x+k•2x+1>0恒成立,即k>-2x-2-x恒成立,
因为-2x-2-x=-(2x+2-x)≤-2,当且仅当2x=2-x即x=0时取等号,
所以k>-2;
(2) ,
,
令 ,则
,则 ,
,
当k>1时, 无最小值,舍去;
无最小值,舍去;
当k=1时,y=1最小值不是-2,舍去;
当k<1时, ,最小值为
,最小值为 ,
,
综上所述,k=-8.
(3)由题意,f(x1)+f(x2)>f(x3)对任意x1,x2,x3∈R恒成立.
当k>1时,因 且
且 ,
,
故 ,即1<k≤4;
,即1<k≤4;
当k=1时,f(x1)=f(x2)=f(x3)=1,满足条件;
当k<1时, 且
且 ,故
,故 ,解得
,解得 ;
;
综上所述,
点评:本题考查复合函数的单调性、函数恒成立、函数最值等问题,考查转化思想,综合性较强,难度较大.
(2)
 ,令
,令 ,则
,则 ,分k>1,k=1,k<1三种情况进行讨论求出f(x)的最小值,令其为-2即可解得k值;
,分k>1,k=1,k<1三种情况进行讨论求出f(x)的最小值,令其为-2即可解得k值;(3)由题意,f(x1)+f(x2)>f(x3)对任意x1,x2,x3∈R恒成立.当k=1时易判断;当k>1,k<1时转化为函数的最值问题解决即可,借助(2)问结论易求函数的最值;
解答:解:(1)因为4x+2x+1>0,所以f(x)>0恒成立,等价于4x+k•2x+1>0恒成立,即k>-2x-2-x恒成立,
因为-2x-2-x=-(2x+2-x)≤-2,当且仅当2x=2-x即x=0时取等号,
所以k>-2;
(2)
 ,
,令
 ,则
,则 ,
,当k>1时,
 无最小值,舍去;
无最小值,舍去;当k=1时,y=1最小值不是-2,舍去;
当k<1时,
 ,最小值为
,最小值为 ,
,综上所述,k=-8.
(3)由题意,f(x1)+f(x2)>f(x3)对任意x1,x2,x3∈R恒成立.
当k>1时,因
 且
且 ,
,故
 ,即1<k≤4;
,即1<k≤4;当k=1时,f(x1)=f(x2)=f(x3)=1,满足条件;
当k<1时,
 且
且 ,故
,故 ,解得
,解得 ;
;综上所述,

点评:本题考查复合函数的单调性、函数恒成立、函数最值等问题,考查转化思想,综合性较强,难度较大.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
 .
. 上的最大值和最小值;
上的最大值和最小值; .
. .
. 上的最大值和最小值;
上的最大值和最小值; .
. ,
, 有
有 成立,求
成立,求 的取值范围;
的取值范围; ,对于任意的
,对于任意的 都成立,求
都成立,求 。
。 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 恒成立,求实数
恒成立,求实数