题目内容
设a,b,c是正实数,求证:aabbcc≥(abc)
.
| a+b+c |
| 3 |
证明:不妨设a≥b≥c>0,则lga≥lgb≥lgc.
据排序不等式有:
alga+blgb+clgc≥blga+clgb+algc
alga+blgb+clgc≥clga+algb+blgc
alga+blgb+clgc=alga+blgb+clgc
上述三式相加得:
3(alga+blgb+clgc)≥(a+b+c)(lga+lgb+lgc)
即lg(aabbcc)≥
lg(abc)
故aabbcc≥(abc)
.
据排序不等式有:
alga+blgb+clgc≥blga+clgb+algc
alga+blgb+clgc≥clga+algb+blgc
alga+blgb+clgc=alga+blgb+clgc
上述三式相加得:
3(alga+blgb+clgc)≥(a+b+c)(lga+lgb+lgc)
即lg(aabbcc)≥
| a+b+c |
| 3 |
故aabbcc≥(abc)
| a+b+c |
| 3 |

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
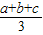 .
.