题目内容
已知四边形PABC为空间四边形，∠PCA=90°，△ABC是边长为
的正三角形，PC=2，D、E分别是PA、AC的中点，BD=
.试判断直线AC与平面BDE的位置关系，并且求出二面角P—AC—B的大小.
解:∵D、E分别是PA、AC的中点， ∴DE∥PC且DE= ∵∠PCA=90°, ∴AC⊥DE. ∵△ABC是边长为 并且E是AC的中点， ∴AC⊥BE,并且BE=3. ∵DE∩BE=E, ∴直线AC与平面DEB垂直. ∴∠DEB为二面角P—AC—B的平面角. 在△BDE中， 由DE=1，BE=3，BD= 得DE2+BE2=BD2，∴∠DEB=90°. 综上所述，直线AC与平面BDE垂直，二面角P—AC—B的大小为90°. 点评:与二面角的棱垂直的平面和二面角的两个面相交的两条射线构成的角就是这个二面角的平面角.利用作与棱垂直的平面得到二面角的方法称为“垂面法”.
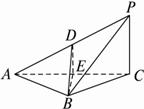
PC=1.
的正三角形，
练习册系列答案
琢玉计划暑假系列答案
小升初重点校各地真题精编卷系列答案
万唯教育非常九年级系列答案
起跑线系列丛书新课标暑假作业系列答案
师大卷王决胜期末100分系列答案
望子成龙最新小学毕业升学必备系列答案
小学升小学毕业升学系统总复习系列答案
新考典中考模拟卷系列答案
新锐复习计划暑假系列答案
相关题目
的正三角形，PC=2，D、E分别是PA、AC的中点，BD=
.试判断直线AC与平面BDE的位置关系，并且求出二面角P-AC-B的大小.
的正三角形，PC=2，D、E分别是PA、AC的中点，BD=
.试判断直线AC与平面BDE的位置关系，并且求出二面角P-AC-B的大小.