题目内容

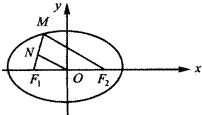
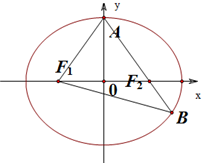
如图，F1、F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，∠F1AF2=60°．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）已知△AF1B的面积为40
3
，求a，b的值．
（Ⅰ）∠F1AF2=60°?a=2c?e=
c
a
=
1
2
．
（Ⅱ）设|BF2|=m，则|BF1|=2a-m，
在三角形BF1F2中，|BF1|2=|BF2|2+|F1F2|2-2|BF2||F1F2|cos120°
?（2a-m）2=m2+a2+am．?m=
3
5
a．
△AF1B面积S=
1
2
|BA||F1A|sin60°
?
1
2
×a×(a+
3
5
a)×
3
2
=40
3

?a=10，
∴c=5，b=5
3
．
练习册系列答案
相关题目
F1，F2是椭圆
x2
9
+
y2
7
=1的两个焦点，A为椭圆上一点，且∠AF1F2=45°，则三角形AF1F2的面积为（　　）
A．7B．
7
4
C．
7
2
D．
7
5
2
如图，椭圆
x2
25
+
y2
9
=1上的点M到焦点F1的距离为2，N为MF1的中点，则|ON|（O为坐标原点）的值为（　　）
A．4B．2C．8D．
3
2
椭圆x2+2y2=6的离心率为（　　）
A．
2
B．
2
2
C．
1
2
D．
3
3
已知F是椭圆5x2+9y2=45的右焦点，P为该椭圆上的动点，A（2，1）是一定点．
（1）求|PA|+
3
2
|PF|的最小值，并求相应点P的坐标；
（2）求|PA|+|PF|的最大值与最小值；
（3）过点F作倾斜角为60°的直线交椭圆于M、N两点，求|MN|；
（4）求过点A且以A为中点的弦所在的直线方程．
已知F1是椭圆
x2
25
+
y2
9
=1的左焦点，P是椭圆上的动点，A（1，1）是一定点，则PA+PF1的最大值为______．
设椭圆
x2
3
+
y2
4
=1的焦点为F1、F2，P为椭圆上一点，且|PF1|=3|PF2|，则|PF1|的值为（　　）
A．3B．1C．
3
3
2
D．
3
2
已知F1，F2是椭圆
x2
k+2
+
y2
k+1
=1的左、右焦点，过F1的直线交椭圆于A，B两点，若△ABF2的周长为8，则k的值为______．
已知F1、F2为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点；M为椭圆上一点，MF1垂直于x轴，且∠F1MF2=60°，则椭圆的离心率为（　　）
A．
1
2
B．
2
2
C．
3
3
D．
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网