题目内容
【题目】已知函数f（x）=x﹣ 
+alnx（a∈R）．
（1）若函数f（x）在[1，+∞）上单调递增，求实数a的取值范围；
（2）已知g（x）= 
x2+（m﹣1）x+ ，m≤﹣ 
，h（x）=f（x）+g（x），当时a=1，h（x）有两个极值点x1 ， x2 ， 且x1＜x2 ， 求h（x1）﹣h（x2）的最小值．
【答案】
（1）解：∵f（x）=x﹣ 
+alnx，
∴f′（x）=1+ 
+ 
，
∵f（x）在[1，+∞）上单调递增，
∴f′（x）=1+ + ≥0在[1，+∞）上恒成立，
∴a≥﹣（x+ ）在[1，+∞）上恒成立，
∵y=﹣x﹣ 在[1，+∞）上单调递减，
∴y≤﹣2，
∴a≥﹣2
（2）解：h（x）=f（x）+g（x）=lnx+ 
x2+mx，其定义域为（0，+∞），
求导得，h′（x）= 
，
若h′（x）=0两根分别为x1，x2，则有x1x2=1，x1+x2=﹣m，
∴x2= 
，从而有m=﹣x1﹣ ，
∵m≤﹣ 
，x1＜x2，
∴x1∈[ 
，1]
则h（x1）﹣h（x2）=h（x1）﹣h（ ）=2lnx1+ （ 
﹣ 
）+（﹣x1﹣ ）（x1﹣ ），
令φ（x）=2lnx﹣ 
（x2﹣ 
），x∈[ 
，1]．
则[h（x1）﹣h（x2）]min=φ（x）min，
φ′（x）=﹣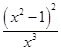 
，
当x∈（ ，1]时，φ′（x）＜0，
∴φ（x）在[ ，1]上单调递减，
φ（x）min=φ（1）=0，
∴h（x1）﹣h（x2）的最小值为0
【解析】（1）利用函数单调性和导数之间的关系进行求解即可．（2）求出函数h（x）的表达式，求出函数h（x）的导数，利用函数极值，最值和导数之间的关系进行求解．
【考点精析】掌握函数的极值与导数是解答本题的根本，需要知道求函数
的极值的方法是:（1）如果在
附近的左侧
,右侧
,那么
是极大值（2）如果在附近的左侧
,右侧
,那么
是极小值．
