题目内容
过点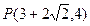 作一条直线和
作一条直线和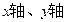 分别相交于
分别相交于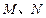 两点,试求
两点,试求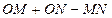 的最大值。(其中
的最大值。(其中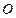 为坐标原点)
为坐标原点)
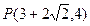 作一条直线和
作一条直线和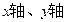 分别相交于
分别相交于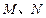 两点,试求
两点,试求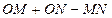 的最大值。(其中
的最大值。(其中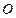 为坐标原点)
为坐标原点) 6
6过点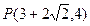 作一圆与
作一圆与 轴、
轴、 轴分别相切于点A、B,且使点
轴分别相切于点A、B,且使点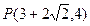
在优弧AB上,则圆的方程为 ,于是过点
,于是过点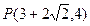 作圆的切线和
作圆的切线和 轴、
轴、 轴分别相交于
轴分别相交于 两点,圆为
两点,圆为 的内切圆,故
的内切圆,故
若过点 的直线
的直线 不和圆相切,则作圆的平行于
不和圆相切,则作圆的平行于 的切线和
的切线和 轴、
轴、 轴分别相交于
轴分别相交于
 两点,则
两点,则 。由折线
。由折线 的长大于
的长大于 的长及切线长定理,得
的长及切线长定理,得

 所以,
所以,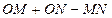 的最大值为6。
的最大值为6。
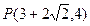 作一圆与
作一圆与 轴、
轴、 轴分别相切于点A、B,且使点
轴分别相切于点A、B,且使点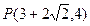
在优弧AB上,则圆的方程为
 ,于是过点
,于是过点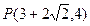 作圆的切线和
作圆的切线和 轴、
轴、 轴分别相交于
轴分别相交于 两点,圆为
两点,圆为 的内切圆,故
的内切圆,故
若过点
 的直线
的直线 不和圆相切,则作圆的平行于
不和圆相切,则作圆的平行于 的切线和
的切线和 轴、
轴、 轴分别相交于
轴分别相交于 两点,则
两点,则 。由折线
。由折线 的长大于
的长大于 的长及切线长定理,得
的长及切线长定理,得
 所以,
所以,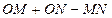 的最大值为6。
的最大值为6。
练习册系列答案
相关题目
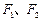 和动点P,
和动点P,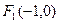 、
、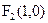 ,动点
,动点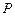 满足
满足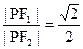 ,动点
,动点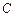 ,曲线
,曲线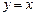 的对称曲线为曲线
的对称曲线为曲线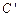 ,直线
,直线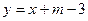 与曲线
与曲线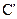 交于A、B两点,O是坐标原点,△ABO的面积为
交于A、B两点,O是坐标原点,△ABO的面积为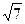 ,
,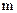 的值。
的值。 与圆
与圆 .求
.求 ,
, 的坐标;
的坐标; 的面积。
的面积。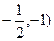 ,求(1)直线BC的方程;(2)弦BC的长度.
,求(1)直线BC的方程;(2)弦BC的长度.
 为圆心的圆与直线
为圆心的圆与直线 相离,则圆的半径
相离,则圆的半径 的取值范围是( ).
的取值范围是( ).


