题目内容
设函数
,则
（ ）
,则 （ ）| A．有最大值 | B．有最小值 | C．是增函数 | D．是减函数 |
A
本题考查函数的性质及均值不等式
由
得
；令
得
，此为函数的一个极大值点，故函数不单调，所以C，D均错.
因为
，所以
，则
且
由均值不等式定理得
，当且仅当
时成立
则
所以
即此函数有最大值，所以正确答案为A
由
得；令得，此为函数的一个极大值点，故函数不单调，所以C，D均错.因为
，所以，则且由均值不等式定理得
，当且仅当时成立则
所以
即此函数有最大值，所以正确答案为A
练习册系列答案
相关题目
，则
( )
的值为_________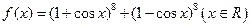 
的最大值等于 .
（
）的图象与反比例函数
图象相交于点
，已知点
的坐标为
，点
在第三象限内，且
的面积为
（
为坐标原点）
的值；
轴的另一个交点为
，
点为线段
在区间
上的最大值为
, 则
等于( )
.则函数
的最大值为 
