题目内容
 某家庭对新购买的商品房进行装潢,设装潢开始后的时间为t(天),室内每立方米空气中甲醛含量为y(毫克).已知在装潢过程中,y与t成正比;在装潢完工后,y与t的平方成反比,如图所示.
某家庭对新购买的商品房进行装潢,设装潢开始后的时间为t(天),室内每立方米空气中甲醛含量为y(毫克).已知在装潢过程中,y与t成正比;在装潢完工后,y与t的平方成反比,如图所示.(Ⅰ)写出y关于t的函数关系式;
(Ⅱ)已知国家对室内甲醛含量的卫生标准是甲醛浓度不超过0.08毫克/立方米.按照这个标准,这个家庭装潢完工后,经过多少天才可以入住?
分析:(Ⅰ)根据题意先设直线OA:y=at,将点A(40,0.5)代入直线方程即得这一段上的函数解析式,再设y=
,将点A(40,0.5)代入,即得另一段上的函数解析式,从而得出y关于t的函数式;
(Ⅱ)由题意得出一个关于x的不等关系,即可解得:按这个标准,这个家庭在装潢后多少天方可入住.
| k |
| t2 |
(Ⅱ)由题意得出一个关于x的不等关系,即可解得:按这个标准,这个家庭在装潢后多少天方可入住.
解答:解:(Ⅰ)设直线OA:y=at,将点A(40,0.5)代入直线方程,得a=
,
即y=
t(0<t≤40)(4分)
设y=
,将点A(40,0.5)代入,得k=800,即y=
(t>40)
(8分)y关于t的函数是y=
(10分)
(Ⅱ)由题意知,
≤0.08,解得x≥100或x≤-100(舍)(13分)
又100-40=60(天)
答:按这个标准,这个家庭在装潢后60天方可入住.(15分)
| 1 |
| 80 |
即y=
| 1 |
| 80 |
设y=
| k |
| t2 |
| 800 |
| t2 |
(8分)y关于t的函数是y=
|
(Ⅱ)由题意知,
| 800 |
| x2 |
又100-40=60(天)
答:按这个标准,这个家庭在装潢后60天方可入住.(15分)
点评:本题考查了分段函数,以及函数与方程的思想,数形结合的思想.属于基础题.

练习册系列答案
相关题目
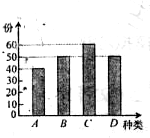 (2012•枣庄一模)学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如图所示.为了了解同学们对新推出的四款套餐的评价,对就餐的每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面的表格所示:
(2012•枣庄一模)学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如图所示.为了了解同学们对新推出的四款套餐的评价,对就餐的每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面的表格所示: 某家庭对新购买的商品房进行装潢,设装潢开始后的时间为t(天),室内每立方米空气中甲醛含量为y(毫克).已知在装潢过程中,y与t成正比;在装潢完工后,y与t的平方成反比,如图所示.
某家庭对新购买的商品房进行装潢,设装潢开始后的时间为t(天),室内每立方米空气中甲醛含量为y(毫克).已知在装潢过程中,y与t成正比;在装潢完工后,y与t的平方成反比,如图所示.