题目内容
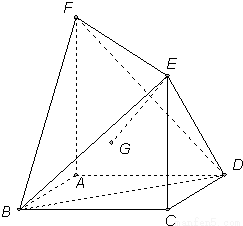
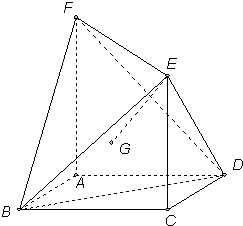 如图ABCD正方形,边长为1,EC⊥平面ABCD,EC∥AF,且λEC=AF(λ>1),
如图ABCD正方形,边长为1,EC⊥平面ABCD,EC∥AF,且λEC=AF(λ>1),(1)证明:BD⊥EF
(2)若EC=1,求二面角B-EF-C平面角的取值范围;
(3)设G是△BDF的重心,试问,是否有可能EG⊥平面BDF,若能求出EC的最小值,若不能,请说明理由.
分析:(1)求出两条直线所在的向量,利用向量的数量积等于0可得两条直线垂直.
(2)分别求出两个平面的发行量,利用向量的有关运算求出向量的夹角的余弦值进而转化为二面角的平面角的余弦值,再结合导数求出余弦值的范围进而转化为平面角的取值范围,即可得到答案.
(3)应该先假设EG⊥平面BDF,则得到一个关于CE长度的表达式,然后利用函数球最值的方法求出CE的最小值.
(2)分别求出两个平面的发行量,利用向量的有关运算求出向量的夹角的余弦值进而转化为二面角的平面角的余弦值,再结合导数求出余弦值的范围进而转化为平面角的取值范围,即可得到答案.
(3)应该先假设EG⊥平面BDF,则得到一个关于CE长度的表达式,然后利用函数球最值的方法求出CE的最小值.
解答: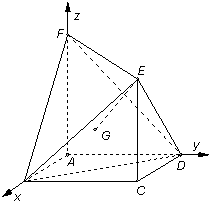 解:(1)方法一:如图建立坐标系,B(1,0,0),D(0,1,0),
解:(1)方法一:如图建立坐标系,B(1,0,0),D(0,1,0),
=(1,-1,0)
设E(1,1,h),那么F(0,0,λh),
所以
=(1,1,h-λh)
•
=0,
所以BD⊥EF.
(2)
=(0,1,1),
=(-1,0,λ),则面BEF得法向量
=(λ,-1,1),平面EFC的法向量是
=(1,-1,0)
所以cos<
,
>=
=
记f(λ)=
(λ>1),
所以f′(λ)=
所以f(λ)在(1,2)是增函数,在(2,+∞)是减函数,
所以f(λ)<f(2)=
,f(λ)=
=
(1+
)>
,而f(1)=
所以
<f(λ)<
,
所以
<cos<
,
>≤
,
二面角B-EF-C平面角的取值范围是[
,
)
(3)B(1,0,0),D(0,1,0),E(1,1,h),F(0,0,λh),
所以G(
,
,
),
=(
,
,h-
)
=(1,-1,0),
=(-1,0,λh),∴
•
=0,
⊥
若EG⊥平面BDF,则
•
=-
+λh(h-
)=0
得h2=
(1<λ<3),
所以当CE2=
(1<λ<3)时,EG⊥平面BDF
此时CE2=
=
≥
,所以ECmin=
 解:(1)方法一:如图建立坐标系,B(1,0,0),D(0,1,0),
解:(1)方法一:如图建立坐标系,B(1,0,0),D(0,1,0),| DB |
设E(1,1,h),那么F(0,0,λh),
所以
| FE |
| DB |
| FE |
所以BD⊥EF.
(2)
| BE |
| BF |
| n |
| DB |
所以cos<
| DB |
| n |
| λ+1 | ||||
|
|
记f(λ)=
| (λ+1)2 |
| 2(λ2+2) |
所以f′(λ)=
| (λ+1)(2-λ) |
| (λ2+2)2 |
所以f(λ)在(1,2)是增函数,在(2,+∞)是减函数,
所以f(λ)<f(2)=
| 3 |
| 4 |
| (λ+1)2 |
| 2(λ2+2) |
| 1 |
| 2 |
| 2λ-1 |
| λ2+2 |
| 1 |
| 2 |
| 2 |
| 3 |
所以
| 1 |
| 2 |
| 3 |
| 4 |
所以
| ||
| 2 |
| DB |
| n |
| ||
| 2 |
二面角B-EF-C平面角的取值范围是[
| π |
| 6 |
| π |
| 4 |
(3)B(1,0,0),D(0,1,0),E(1,1,h),F(0,0,λh),
所以G(
| 1 |
| 3 |
| 1 |
| 3 |
| λh |
| 3 |
| GE |
| 2 |
| 3 |
| 2 |
| 3 |
| λh |
| 3 |
| DB |
| BF |
| GE |
| DB |
| GE |
| DB |
若EG⊥平面BDF,则
| GE |
| BF |
| 2 |
| 3 |
| λh |
| 3 |
得h2=
| 2 |
| 3λ-λ2 |
所以当CE2=
| 2 |
| 3λ-λ2 |
此时CE2=
| 2 |
| 3λ-λ2 |
| 2 | ||||
-(λ-
|
| 8 |
| 9 |
2
| ||
| 3 |
点评:解决此类问题的关键是熟练掌握几何体的结构特征,以便建立坐标系进而利用向量求出有关问题的表达式,再结合导数或者函数解析式的特征求其最值即可.

练习册系列答案
相关题目
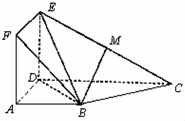 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点. 如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.