题目内容
【题目】已知
，函数
的最小值为1.
(1)求
的值；
(2)若
，求实数
的最大值.
【答案】（1）
（2）
【解析】【试题分析】（1）运用绝对值的三角不等式
或运用绝对值的定义将其化归为分段函数的最值问题来处理，求解时借助分段函数的单调性可知
在
上单调递减， 
在
上单调递增，从而探求出
在
处取最小值；（2）先将不等式中的参数
分离出来得到
，再运用基本不等式或柯西不等式求
最值：
（1）法一： 
，
∵
且
，
∴
，当
时取等号，即
的最小值为
，
∴
；
法二：∵
， ∴
，
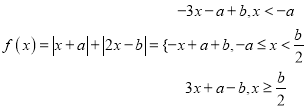显然
在
上单调递减， 
在
上单调递增，
∴
的最小值为
， ∴
；
（2）法一：∵
恒成立，∴
恒成立，
，
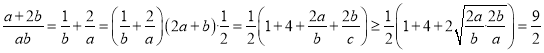当
时， 
取得最小值
， ∴
，即实数
的最大值为
；
法二：∵
恒成立， ∴
恒成立， 
恒成立， 
， ∴
，即实数
的最大值为
．
期末金牌卷系列答案
轻松课堂标准练系列答案【题目】某高职院校进行自主招生文化素质考试，考试内容为语文、数学、英语三科，总分为200分.现从上线的考生中随机抽取20人，将其成绩用茎叶图记录如下：
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
（Ⅰ）计算上线考生中抽取的男生成绩的方差
；（结果精确到小数点后一位）
（Ⅱ）从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会，求所选考生恰为一男一女的概率.
【题目】在“一带一路”的建设中，中石化集团获得了某地深海油田区块的开采权，集团在该地区随机初步勘探了几口井，取得了地质资料.进入全面勘探时期后，集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高，如果新设计的井位与原有井位重合或接近，便利用旧井的地质资料，不必打这口新井，以节约勘探费用.勘探初期数据资料下表：
井号I | 1 | 2 | 3 | 4 | 5 | 6 |
坐标 |
|
|
|
|
|
|
钻探深度 | 2 | 4 | 5 | 6 | 8 | 10 |
出油量 | 40 | 70 | 110 | 90 | 160 | 205 |
（1）在散点图中
号旧井位置大致分布在一条直线附近，借助前5组数据求得回归线方程为
，求
，并估计
的预报值；
（2）现准备勘探新井
，若通过1、3、5、7号井计算出的
的值（
精确到0.01）相比于（1）中
的值之差（即： 
）不超过10%，则使用位置最接近的已有旧井
，否则在新位置打井，请判断可否使用旧井？（参考公式和计算结果：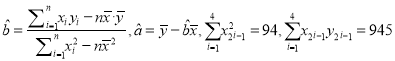 
）
（3）设出油量与钻探深度的比值
不低于20的勘探井称为优质井，在原有井号
的井中任意勘探3口井，求恰好2口是优质井的概率．
