题目内容
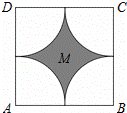
如图，在边长为2的正方形ABCD内随机取一点P，分别以A、B、C、D为圆心、1为半径作圆，在正方形ABCD内的四段圆弧所围成的封闭区域记为M（阴影部分），则点P取自区域M的概率是（ ）
|
| A． |
| B． |
| C． |
| D． |
|
考点：
几何概型．
专题：
概率与统计．
分析：
由题意知本题是一个几何概型，试验发生包含的所有事件是正方形面积S=2×2，而阴影部分区域可以看作是由边长为2的正方形面积减去半径为1的圆的面积得到，最后利用几何概型的概率公式解之即可．
解答：
解：由题意知本题是一个几何概型，
∵试验发生包含的所有事件是矩形面积S=2×2=4，
阴影部分区域的面积是4﹣π，
∴由几何概型公式得到P=
=1﹣
，
故选C．
点评：
本题主要考查了几何概型，解题的关键求阴影部分的面积，同时考查了计算能力，属于中档题．
练习册系列答案
相关题目
（2013•资阳模拟）如图，在边长为2的正六边形ABCDEF中，P是△CDE内（含边界）的动点，设向量
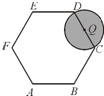如图，在边长为2的正六边形ABCDEF中，动圆Q的半径为1，圆心在线段CD（含端点）上运动，P是圆Q上及内部的动点，设向量| AP |
| AB |
| AF |
| A、（1，2] |
| B、[5，6] |
| C、[2，5] |
| D、[3，5] |
的起点、终点和模;
共线的向量;
相等的向量.