题目内容
已知函数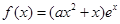 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)当 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围.
的取值范围.
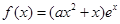 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.(1)当
 时,解不等式
时,解不等式 ;
;(2)当
 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程 在[k,k+1]上有解;
在[k,k+1]上有解;(3)若
 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围.
的取值范围.⑴因为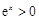 ,所以不等式
,所以不等式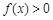 即为
即为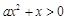 ,
,
又因为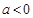 ,所以不等式可化为
,所以不等式可化为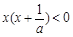 ,
,
所以 不等式
不等式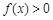 的解集为
的解集为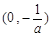 .………………………………………4分
.………………………………………4分
⑵当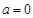 时, 方程即为
时, 方程即为 ,由于
,由于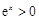 ,所以
,所以 不是方程的解,
不是方程的解,
所以原方程等价于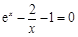 ,令
,令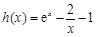 ,
,
因 为
为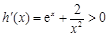 对于
对于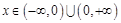 恒成立,
恒成立,
所以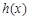 在
在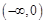 和
和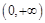 内是单调增函数,……………………………6分
内是单调增函数,……………………………6分
又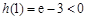 ,
,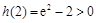 ,
,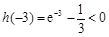 ,
,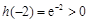 ,
,
所以方程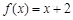 有且只有两个实数根,且分别在区间
有且只有两个实数根,且分别在区间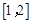 和
和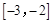 上,
上,
所以整数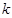 的所有值为
的所有值为 .……………………………………………8分
.……………………………………………8分
⑶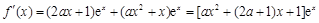 ,
,
①当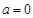 时,
时,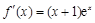 ,
,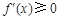 在
在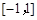 上恒成立,当且仅当
上恒成立,当且仅当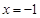 时
时
取等号,故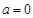
 符合要求;………………………………………………………10分
符合要求;………………………………………………………10分
②当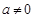 时,令
时,令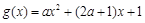 ,因为
,因为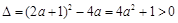 ,
,
所以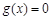 有两个不相等的实数根
有两个不相等的实数根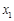 ,
,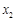 ,不妨设
,不妨设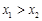 ,
,
因此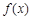 有极大值又有极小值.
有极大值又有极小值.
若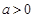 ,因为
,因为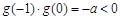 ,所以
,所以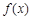 在
在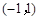 内有极值点,
内有极值点,
故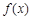 在
在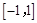 上不单调.………………………………………………………12分
上不单调.………………………………………………………12分
若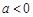 ,可知
,可知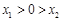 ,
,
因为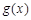 的图象开口向下,要使
的图象开口向下,要使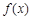 在
在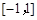 上单调,因为
上单调,因为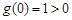 ,
,
必须满足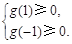 即
即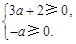 所以
所以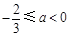 .--------------------------14分
.--------------------------14分
综上可知,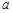 的取值范围是
的取值范围是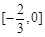 .………………………………………16分
.………………………………………16分
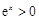 ,所以不等式
,所以不等式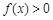 即为
即为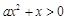 ,
,又因为
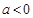 ,所以不等式可化为
,所以不等式可化为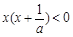 ,
,所以
 不等式
不等式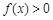 的解集为
的解集为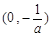 .………………………………………4分
.………………………………………4分⑵当
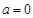 时, 方程即为
时, 方程即为 ,由于
,由于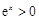 ,所以
,所以 不是方程的解,
不是方程的解,所以原方程等价于
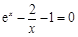 ,令
,令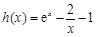 ,
,因
 为
为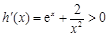 对于
对于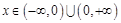 恒成立,
恒成立,所以
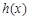 在
在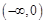 和
和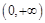 内是单调增函数,……………………………6分
内是单调增函数,……………………………6分又
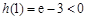 ,
,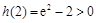 ,
,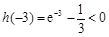 ,
,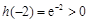 ,
,所以方程
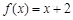 有且只有两个实数根,且分别在区间
有且只有两个实数根,且分别在区间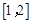 和
和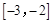 上,
上,所以整数
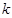 的所有值为
的所有值为 .……………………………………………8分
.……………………………………………8分⑶
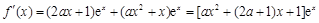 ,
,①当
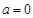 时,
时,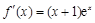 ,
,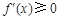 在
在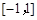 上恒成立,当且仅当
上恒成立,当且仅当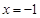 时
时取等号,故
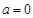
 符合要求;………………………………………………………10分
符合要求;………………………………………………………10分②当
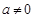 时,令
时,令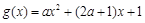 ,因为
,因为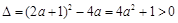 ,
,所以
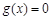 有两个不相等的实数根
有两个不相等的实数根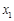 ,
,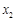 ,不妨设
,不妨设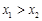 ,
,因此
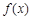 有极大值又有极小值.
有极大值又有极小值.若
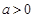 ,因为
,因为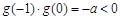 ,所以
,所以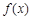 在
在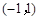 内有极值点,
内有极值点,故
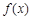 在
在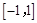 上不单调.………………………………………………………12分
上不单调.………………………………………………………12分若
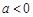 ,可知
,可知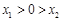 ,
,因为
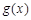 的图象开口向下,要使
的图象开口向下,要使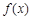 在
在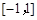 上单调,因为
上单调,因为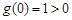 ,
,必须满足
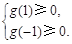 即
即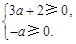 所以
所以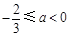 .--------------------------14分
.--------------------------14分综上可知,
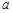 的取值范围是
的取值范围是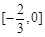 .………………………………………16分
.………………………………………16分略

练习册系列答案
相关题目
 为
为 的各位数字之和,如
的各位数字之和,如 ,则
,则 记
记 则
则 =
=  和
和 的图象的对称轴完全相同。若
的图象的对称轴完全相同。若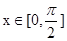 ,则
,则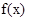 的取值范围是 .
的取值范围是 .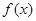 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意 ,有
,有 ,
, ,则称
,则称 上的1级类增函数
上的1级类增函数 上的1级类增函数
上的1级类增函数 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2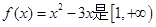 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为
 的图象恰好经过k个格点,则称函数
的图象恰好经过k个格点,则称函数 ;②
;② ;③
;③ ;④
;④ .则其中为一阶格点函数的序号为 .(写出所有正确命题的序号)
.则其中为一阶格点函数的序号为 .(写出所有正确命题的序号)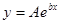 ,可作变换U= ,C= 得到线性回归方程U=C+bx。
,可作变换U= ,C= 得到线性回归方程U=C+bx。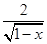 的定义域是
的定义域是 ,1)
,1)


 ,则
,则 的值为( )
的值为( )


 元(叫做税率
元(叫做税率 ),则每年销售量将减少
),则每年销售量将减少 万瓶,如果要使每年在此项经营中所收取的附加税额不少于112万元,则
万瓶,如果要使每年在此项经营中所收取的附加税额不少于112万元,则