题目内容
下列关于曲线 与曲线
与曲线 (5<m<9)几何性质的叙述,正确的有 .(填上你认为正确的序号)①焦距相等 ②离心率相等 ③焦点相同 ④准线相同.
(5<m<9)几何性质的叙述,正确的有 .(填上你认为正确的序号)①焦距相等 ②离心率相等 ③焦点相同 ④准线相同.
【答案】分析:分别确定曲线的几何量,求出相应的性质,即可得到结论.
解答:解:曲线 中,a2=10-m,b2=6-m,c2=a2-b2=4,焦点在x轴上,
中,a2=10-m,b2=6-m,c2=a2-b2=4,焦点在x轴上, ,准线方程为x=±
,准线方程为x=± =±
=± ;
;
曲线 (5<m<9)中,a′2=9-m,b′2=m-5,c′2=a′2+b′2=4,焦点在y轴上,
(5<m<9)中,a′2=9-m,b′2=m-5,c′2=a′2+b′2=4,焦点在y轴上, ,准线方程为x=±
,准线方程为x=± =±
=±
∴两曲线焦距相等,离心率、焦点坐标、准线方程均不相同
故答案为:①
点评:本题考查椭圆、双曲线的几何性质,考查学生的计算能力,确定几何量是关键.
解答:解:曲线
 中,a2=10-m,b2=6-m,c2=a2-b2=4,焦点在x轴上,
中,a2=10-m,b2=6-m,c2=a2-b2=4,焦点在x轴上, ,准线方程为x=±
,准线方程为x=± =±
=± ;
;曲线
 (5<m<9)中,a′2=9-m,b′2=m-5,c′2=a′2+b′2=4,焦点在y轴上,
(5<m<9)中,a′2=9-m,b′2=m-5,c′2=a′2+b′2=4,焦点在y轴上, ,准线方程为x=±
,准线方程为x=± =±
=±
∴两曲线焦距相等,离心率、焦点坐标、准线方程均不相同
故答案为:①
点评:本题考查椭圆、双曲线的几何性质,考查学生的计算能力,确定几何量是关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
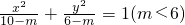 与曲线
与曲线 (5<m<9)几何性质的叙述,正确的有________.(填上你认为正确的序号)①焦距相等 ②离心率相等 ③焦点相同 ④准线相同.
(5<m<9)几何性质的叙述,正确的有________.(填上你认为正确的序号)①焦距相等 ②离心率相等 ③焦点相同 ④准线相同. 与曲线
与曲线 (5<m<9)几何性质的叙述,正确的有 .(填上你认为正确的序号)①焦距相等 ②离心率相等 ③焦点相同 ④准线相同.
(5<m<9)几何性质的叙述,正确的有 .(填上你认为正确的序号)①焦距相等 ②离心率相等 ③焦点相同 ④准线相同.