题目内容
设p:实数x满足 <0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且
<0,其中a<0;q:实数x满足x2-x-6≤0或x2+2x-8>0,且 p是
p是 q的必要不充分条件,求a的取值范围.
q的必要不充分条件,求a的取值范围.
【答案】
a≤-4或- ≤a<0
≤a<0
【解析】
试题分析:解:设A={x|x2-4ax+3a2<0,a<0}={x|3a<x<a,a<0},
B={x|x2-x-6≤0或x2+2x-8>0}={x|-2≤x≤3}∪{x|x<-4或x>2}={x|x<-4或x≥-2}.
4分
由 p是
p是 q的必要不充分条件,转化成它的逆否命题q是p的必要不充分条件,即p 是q的充分不必要条件,也就是p
q的必要不充分条件,转化成它的逆否命题q是p的必要不充分条件,即p 是q的充分不必要条件,也就是p q且q
q且q p.
p.
由A B,得
B,得 或
或 解得a≤-4或-
解得a≤-4或- ≤a<0.
≤a<0.
考点:充分条件与必要条件
点评:充分条件与必要条件是一个重要的考点。当 时,A是B的充分不必要条件;当
时,A是B的充分不必要条件;当 时,A是B的必要不充分条件;当
时,A是B的必要不充分条件;当 时,A是B的充要条件;当
时,A是B的充要条件;当 时,A是B的既不充分也不必要条件。
时,A是B的既不充分也不必要条件。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)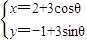 (θ为参数),直线l的方程为x-3y+2=0,则曲线C上的动点P(x,y)到直线l距离的最大值为 .
(θ为参数),直线l的方程为x-3y+2=0,则曲线C上的动点P(x,y)到直线l距离的最大值为 .