题目内容
圆C:(x-2)2+(y-3)2=4,则P(3,2)( )A.是圆心
B.在圆C外
C.在圆C内
D.在圆C上
【答案】分析:圆C:(x-2)2+(y-3)2=4,的圆心C(2,3),半径r=2,由此求出|PC|的长并和半径相比较,能求出结果.
解答:解:∵圆C:(x-2)2+(y-3)2=4,
∴圆C的圆心C(2,3),半径r=2,
∵P(3,2),
∴|PC|=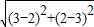 =
=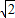 ,
,
∵|PC|=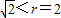 ,
,
∴P(3,2)在圆C内.
故选C.
点评:本题考查点与圆的位置关系,若点到圆心的距离小于半径,则点在圆内;若点到圆心的距离等于半径,则点在圆上;若点到圆心的距离大于半径,则点在圆外.
解答:解:∵圆C:(x-2)2+(y-3)2=4,
∴圆C的圆心C(2,3),半径r=2,
∵P(3,2),
∴|PC|=
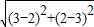 =
=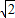 ,
,∵|PC|=
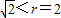 ,
,∴P(3,2)在圆C内.
故选C.
点评:本题考查点与圆的位置关系,若点到圆心的距离小于半径,则点在圆内;若点到圆心的距离等于半径,则点在圆上;若点到圆心的距离大于半径,则点在圆外.

练习册系列答案
相关题目