题目内容

如果直线y=kx+1与圆x²+y²+kx+my-4=0相交于M、N两点，且点M、N关于直线x+y=0对称，则不等式组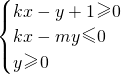 $数学公式$ 所表示的平面区域的面积为________．

$\text{[math]}$
分析：由M与N关于x+y=0对称得到直线y=kx+1与x+y=0垂直，利用两直线垂直时斜率的乘积为-1，得到k的值；设出M与N的坐标，然后联立y=x+1与圆的方程，消去y得到关于x的一元二次方程，根据韦达定理得到两横坐标之和的关于m的关系式，再根据MN的中点在x+y=0上得到两横坐标之和等于-1，列出关于m的方程，求出方程的解得到m的值，把k的值和m的值代入不等式组，在数轴上画出相应的平面区域，求出面积即可．
解答：

解：∵M、N两点，关于直线x+y=0对称，
∴k=1，又圆心 $\text{[math]}$ 在直线x+y=0上
∴ $\text{[math]}$
∴m=-1
∴原不等式组变为 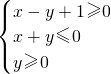$\text{[math]}$ 作出不等式组表示的平面区域，
△AOB为不等式所表示的平面区域，联立 $\text{[math]}$ 解得B（- $\text{[math]}$ ， $\text{[math]}$ ），A（-1，0），
所以S_△AOB= $\text{[math]}$ ×|-1|×|- $\text{[math]}$ |= $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：此题考查学生掌握直线与圆的位置关系、二元一次不等式（组）与平面区域等基本知识，考查学生灵活运用中点坐标公式化简求值，会进行简单的线性规划，是一道中档题．