题目内容
已知函数 .
.
(1)求 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)若 在区间
在区间 上的最大值与最小值的和为
上的最大值与最小值的和为 ,求
,求 的值.
的值.
 .
.(1)求
 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;(2)若
 在区间
在区间 上的最大值与最小值的和为
上的最大值与最小值的和为 ,求
,求 的值.
的值.(1) ,
, ;(2)
;(2)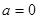
 ,
, ;(2)
;(2)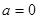
试题分析:(1)先逆用正弦的二倍角公式和降幂公式,并将函数解析式化为
 的形式,再利用
的形式,再利用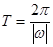 确定周期,利用复合函数的单调性求递减区间;(2)由
确定周期,利用复合函数的单调性求递减区间;(2)由 ,确定
,确定 的范围,然后结合函数
的范围,然后结合函数 的图象确定函数
的图象确定函数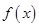 的最大值与最小值,进而根据最大值与最小值的和为
的最大值与最小值,进而根据最大值与最小值的和为 列方程求
列方程求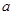 .
.试题解析:(1)
 =
=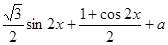 =
=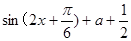 ,∴
,∴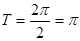 ,由
,由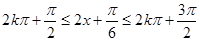 ,解得
,解得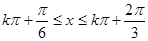 ,∴
,∴ 的单调递减区间为
的单调递减区间为 ;
;(2)∵
 ,∴
,∴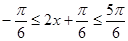 ,∴
,∴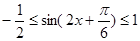 ,
,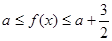 ,∴
,∴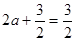
∴
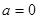 .
.
练习册系列答案
相关题目
 的三个内角A,B,C的对边,
的三个内角A,B,C的对边,
 时,求
时,求 的取值范围.
的取值范围. 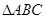 是锐角三角形,
是锐角三角形,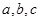 分别是内角
分别是内角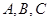 所对边长,并且
所对边长,并且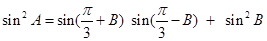 .
.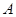 的值;
的值;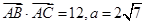 ,求
,求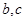 (其中
(其中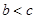 ).
). 中,
中,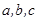 是角A,B,C的对边,若
是角A,B,C的对边,若 ,则
,则 ( )
( )



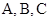 三点共线,且
三点共线,且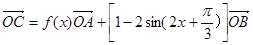 ,则对于函数
,则对于函数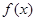 ,下列结论中错误的是( )
,下列结论中错误的是( )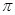
 是函数的一个对称点
是函数的一个对称点 上单调递增
上单调递增 且
且 则
则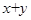 的可能取值是( )
的可能取值是( ) B
B 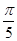 C.
C.  D.
D. 
 ,则
,则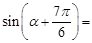 .
.  ,则
,则