Question

若不等式x²-log_mx＜0在（0，

1

2

）内恒成立，则实数m的取值范围为

[

1

16

，1）

．

Answer 1

分析：把已知的不等式变形，转化为一个二次函数和一个对数函数的图象高低问题，然后列出不等式求解m的取值范围．

解答：解：由x²-log_mx＜0，得x²＜log_mx，在同一坐标系中作y=x²和y=log_mx的草图，如图所示

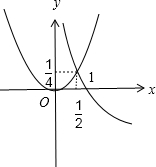
要使x²＜log_mx在（0，

1

2

）内恒成立，只要y=log_mx在（0，

1

2

）内的图象在y=x²的上方，
于是0＜m＜1
∵x=

1

2

时，y=x2=

1

4

∴只要x=

1

2

时，y=logm

1

2

≥

1

4

=logmm

1

4

，
∴

1

2

≤m

1

4

，即

1

16

≤m．
又0＜m＜1，
∴

1

16

≤m＜1．
即实数m的取值范围是[

1

16

，1)．

点评：本题考查了恒成立问题，考查了数形结合的解题思想方法和数学转化思想方法，正确画出图象是解答该题的关键，是中档题．