题目内容
在矩形ABCD中,边AB、AD的长分别为2、1,若M、N分别是边BC、CD上的点,且满足 ,则
,则 的取值范围是________.
的取值范围是________.
[1,4]
分析:先以 所在的直线为x轴,以
所在的直线为x轴,以 所在的直线为x轴,建立坐标系,写出要用的点的坐标,根据两个点的位置得到坐标之间的关系,表示出两个向量的数量积,根据动点的位置得到自变量的取值范围,做出函数的范围,即要求得数量积的范围.
所在的直线为x轴,建立坐标系,写出要用的点的坐标,根据两个点的位置得到坐标之间的关系,表示出两个向量的数量积,根据动点的位置得到自变量的取值范围,做出函数的范围,即要求得数量积的范围.
解答: 解:以
解:以 所在的直线为x轴,以
所在的直线为x轴,以 所在的直线为x轴,建立坐标系如图,
所在的直线为x轴,建立坐标系如图,
∵AB=2,AD=1,
∴A(0,0),B(2,0),C(2,1),D(0,1),
设M(2,b),N(x,1),
∵ ,
,
∴b=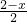
∴ ,
, =(2,
=(2,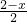 ),
),
∴ =
= ,
,
∴1 ,
,
即1≤ ≤4
≤4
故答案为:[1,4]
点评:本题主要考查平面向量的基本运算,概念,平面向量的数量积的运算,本题解题的关键是表示出两个向量的坐标形式,利用函数的最值求出数量积的范围,本题是一个中档题目.
分析:先以
 所在的直线为x轴,以
所在的直线为x轴,以 所在的直线为x轴,建立坐标系,写出要用的点的坐标,根据两个点的位置得到坐标之间的关系,表示出两个向量的数量积,根据动点的位置得到自变量的取值范围,做出函数的范围,即要求得数量积的范围.
所在的直线为x轴,建立坐标系,写出要用的点的坐标,根据两个点的位置得到坐标之间的关系,表示出两个向量的数量积,根据动点的位置得到自变量的取值范围,做出函数的范围,即要求得数量积的范围.解答:
 解:以
解:以 所在的直线为x轴,以
所在的直线为x轴,以 所在的直线为x轴,建立坐标系如图,
所在的直线为x轴,建立坐标系如图,∵AB=2,AD=1,
∴A(0,0),B(2,0),C(2,1),D(0,1),
设M(2,b),N(x,1),
∵
 ,
,∴b=
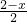
∴
 ,
, =(2,
=(2,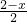 ),
),∴
 =
= ,
,∴1
 ,
,即1≤
 ≤4
≤4故答案为:[1,4]
点评:本题主要考查平面向量的基本运算,概念,平面向量的数量积的运算,本题解题的关键是表示出两个向量的坐标形式,利用函数的最值求出数量积的范围,本题是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
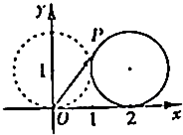 (1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
(1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时, ,则
,则 的坐标为______.
的坐标为______.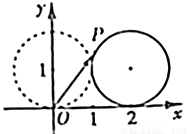
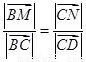 ,则
,则 的取值范围是________.
的取值范围是________. ,则
,则 的取值范围是 .
的取值范围是 .