题目内容
(理)如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点 E在线段PC上,设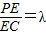 ,PA=AB.
,PA=AB.(I)证明:BD⊥PC;
(Ⅱ)当λ为何值时,PC⊥平面BDE;
(Ⅲ)在(Ⅱ)的条件下,求二面角B-PC-A的平面角大小.
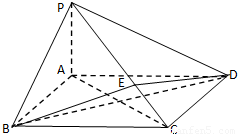
【答案】分析:(Ⅰ)要证BD⊥PC,只要证BD垂直于PC所在的平面PAC即可,由已知底面ABCD为正方形,PA⊥平面ABCD,利用线面垂直的判定即可得证;
(Ⅱ)由PC⊥平面BDE,得到PC⊥OE,利用直角三角形相似即可求出EC,从而求得λ的值;
(Ⅲ)由(Ⅱ)可知∠BEO为二面角B-PC-A的平面角,直接解直角三角形即可得到答案.
解答: (Ⅰ)证明,如图,
(Ⅰ)证明,如图,
∵底面ABCD为正方形,∴AC⊥BD,又PA⊥平面ABCD,∴PA⊥BD
∵PA∩AC=A,∴BD⊥面PAC,∴BD⊥PC;
(Ⅱ)解:若PC⊥平面BDE,则PC⊥OE,
∴△PAC∽△OEC,
∵底面ABCD为正方形,PA=AB,
设PA=AB=a,则AC= a,OC=
a,OC= ,
, .
.
∴ ,即
,即 ,∴
,∴ .
.
则 .
.
所以,当λ等于2时,PC⊥平面BDE;
(Ⅲ)解:当PC⊥平面BDE时,∠BEO为二面角B-PC-A的平面角,
在Rt△CEO中, .
.
在Rt△BOE中, .
.
所以∠BEO= .
.
点评:本题考查了直线与平面垂直的判定与性质,考查了二面角的平面角的求法,考查了学生的空间想象和思维能力,是中档题.
(Ⅱ)由PC⊥平面BDE,得到PC⊥OE,利用直角三角形相似即可求出EC,从而求得λ的值;
(Ⅲ)由(Ⅱ)可知∠BEO为二面角B-PC-A的平面角,直接解直角三角形即可得到答案.
解答:
 (Ⅰ)证明,如图,
(Ⅰ)证明,如图,∵底面ABCD为正方形,∴AC⊥BD,又PA⊥平面ABCD,∴PA⊥BD
∵PA∩AC=A,∴BD⊥面PAC,∴BD⊥PC;
(Ⅱ)解:若PC⊥平面BDE,则PC⊥OE,
∴△PAC∽△OEC,
∵底面ABCD为正方形,PA=AB,
设PA=AB=a,则AC=
 a,OC=
a,OC= ,
, .
.∴
 ,即
,即 ,∴
,∴ .
.则
 .
.所以,当λ等于2时,PC⊥平面BDE;
(Ⅲ)解:当PC⊥平面BDE时,∠BEO为二面角B-PC-A的平面角,
在Rt△CEO中,
 .
.在Rt△BOE中,
 .
.所以∠BEO=
 .
.点评:本题考查了直线与平面垂直的判定与性质,考查了二面角的平面角的求法,考查了学生的空间想象和思维能力,是中档题.

练习册系列答案
相关题目
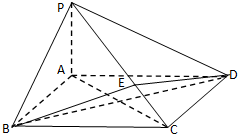 (理)如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点 E在线段PC上,设
(理)如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点 E在线段PC上,设

