Question

预算用2000元购买单件为50元的桌子和20元的椅子，希望使桌椅的总数尽可能的多，但椅子不少于桌子数，且不多于桌子数的1  5倍，问桌、椅各买多少才行？

Answer 1

命题意图  利用线性规划的思想方法解决某些实际问题属于直线方程的一个应用，本题主要考查找出约束条件与目标函数、准确地描画可行域，再利用图形直观求得满足题设的最优解 

知识依托  约束条件，目标函数，可行域，最优解 

错解分析  解题中应当注意到问题中的桌、椅张数应是自然数这个隐含条件，若从图形直观上得出的最优解不满足题设时，应作出相应地调整，直至满足题设 

技巧与方法  先设出桌、椅的变数后，目标函数即为这两个变数之和，再由此在可行域内求出最优解 

解  设桌椅分别买x,y张，把所给的条件表示成不等式组，即约束条件

为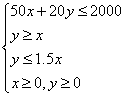由

∴A点的坐标为(，)

由

∴B点的坐标为(25，)

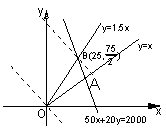
所以满足约束条件的可行域是以A(，)，B(25，)，O(0，0)为顶点的三角形区域(如右图)

由图形直观可知，目标函数z=x+y在可行域内的最优解为(25，)，但注意到x∈N,y∈N^*,故取y=37 

故有买桌子25张，椅子37张是最好选择