题目内容
设a>0。(1)证明:![]() 取得极大值极小值的点各有一个;
取得极大值极小值的点各有一个;
(2)当极大值为1,极小值为-1时,求a、b的值。
答案:
解析:
解析:
(1)证明: 令f ¢ (x)=0即ax2+2bx-a=0 (*) ∵ D=4b2+4a2>0,故方程有两个不相等的实根,为x1,x2,故不妨设x1<x2,f ¢(x)=a(x-x1)(x-x2) f(x),f ¢(x)的变化情况如下表
由表可知极大值和极小值的点各一个。 (2)由(1)可知 可得:x22-x12=a(x1+x2)+2b (*) 又
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


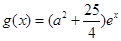 ,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围
,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围