题目内容
(本小题共12分)
设x=3是函数f (x) = (x2+ax+b)·e3-x (x∈R)的一个极值点。
⑴求a与b的关系式,(用a表示b),并求f(x)的单调区间。
⑵设a>0,
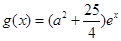 ,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围
,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围
(1) 当a<-4时,x2>3=x1,则在区间(-∞,3)上, ,f(x)为减函数;
,f(x)为减函数;
在区间(3,-a-1)上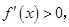 f (x)为增函数。
f (x)为增函数。
在区间(-a-1,+∞)上 f (x)为减函数。
f (x)为减函数。
当a>-4时,x2<3=x1,则在区间(-∞,-a-1)上 f(x)为减函数;
f(x)为减函数;
在区间(-a-1,3)上,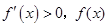 为增函数;
为增函数;
在区间(3,+∞)上, f(x)为减函数。
f(x)为减函数。
(2) 
【解析】解:⑴ (2分)
(2分)


=
令
由于x=3是极值点,所以3+a+1≠0,那么a≠-4。
当a<-4时,x2>3=x1,则在区间(-∞,3)上, ,f(x)为减函数;
,f(x)为减函数;
在区间(3,-a-1)上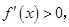 f (x)为增函数。
f (x)为增函数。
在区间(-a-1,+∞)上 f (x)为减函数。
(4分)
f (x)为减函数。
(4分)
当a>-4时,x2<3=x1,则在区间(-∞,-a-1)上 f(x)为减函数;
f(x)为减函数;
在区间(-a-1,3)上,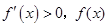 为增函数;
为增函数;
在区间(3,+∞)上, f(x)为减函数。
(6分)
f(x)为减函数。
(6分)
⑵由①知,当a>0时,f(x)在区间(0,3)上的单调递增,在区间(3,4)上单调递减,
那么f(x)在区间[0,4]上的值域是[min (f (0),f (4)),f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f(3)=a+6,
那么f(x)在区间[0,4]上的值域是[-(2a+3)e3,a+6], (8分)
又g (x)= 在区间[0,4]上是增函数,
在区间[0,4]上是增函数,
且它在区间[0,4]上的值域是 (10分)
(10分)
由于
所以只需
故a的取值范围是 。
(12分
。
(12分

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案 ⊥平面
⊥平面 ,
, ∥
∥ 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点
 ∥平面
∥平面 ;
; .
. 名,女同学有
名,女同学有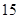 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个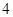 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;


 ,
, ,求证:
,求证: .
. 的值.
的值.