题目内容
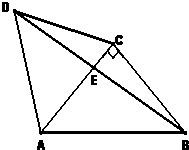 如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.
如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.(1)求cos∠CBE的值;
(2)求AE.
分析:(1)根据图中各角和边的关系可得∠CBE的值,再由两角差的余弦公式可得答案.
(2)根据正弦定理可直接得到答案.
(2)根据正弦定理可直接得到答案.
解答:解:.(1)∵∠BCD=90°+60°=150°,CB=AC=CD
∴∠CBE=15°,∴cos∠CBE=cos(45°-30°)=
.
(2)在△ABE中,AB=2,由正弦定理得
=
,
故AE=
=
=
-
.
∴∠CBE=15°,∴cos∠CBE=cos(45°-30°)=
| ||||
| 4 |
(2)在△ABE中,AB=2,由正弦定理得
| AE |
| sin(45°-15°) |
| 2 |
| sin(90°+15°) |
故AE=
| 2sin30° |
| cos15° |
2×
| ||||||
|
| 6 |
| 2 |
点评:本题主要考查正弦定理及平面几何知识的应用.解三角形一直是高考的重点内容之一,不能轻视.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
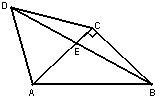 如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2,则AE=
如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2,则AE=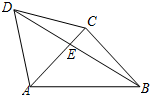 如图,△ACD是等边三角形,△ABC是等腰直角三角形∠ACB=90°,BD交AC于E,AB=2.
如图,△ACD是等边三角形,△ABC是等腰直角三角形∠ACB=90°,BD交AC于E,AB=2. 如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.
如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.