题目内容
已知函数![]()
![]()
![]()
(Ⅰ)证明:曲线![]()
(Ⅱ)若![]() 求a的取值范围。
求a的取值范围。
【思路点拨】第(I)问直接利用导数的几何意义,求出切线的斜率,然后易写出直接方程。
(II)第(II)问是含参问题,关键是抓住方程![]() 的判别式进行分类讨论.
的判别式进行分类讨论.
【精讲精析】解:(I)![]() .
.
由![]() 得曲线
得曲线![]() 在x=0处的切线方程为
在x=0处的切线方程为
![]()
由此知曲线![]() 在x=0处的切线过点(2,2)。
在x=0处的切线过点(2,2)。
(II)由![]() 得
得![]()
(i)当![]() 时,
时,![]() 没有极小值;
没有极小值;
(ii)当![]() 或
或![]() 时,由
时,由![]() 得
得
![]()
故![]() 。由题设知
。由题设知![]() ,
,
当![]() 时,不等式
时,不等式![]() 无解;
无解;
当![]() 时,解不等式
时,解不等式![]() 得
得![]()
综合(i)(ii)得![]() 的取值范围是
的取值范围是![]() 。
。

练习册系列答案
相关题目
 , 已知函数
, 已知函数
 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;  在点
在点 处的切线相互平行, 且
处的切线相互平行, 且 证明
证明 .
.


 ,求
,求 的取值范围。
的取值范围。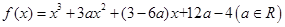
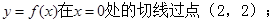
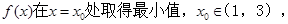 求a的取值范围.
求a的取值范围. ,证明:
,证明: 是偶函数; (2)
是偶函数; (2) 上是增函数。
上是增函数。