题目内容
已知函数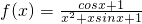 ,对于区间
,对于区间 上的任意实数x1、x2,有如下条件:
上的任意实数x1、x2,有如下条件:
①x1>x2;②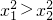 ;③|x1|>x2;④x1+x2<0;⑤x1>|x2|.
;③|x1|>x2;④x1+x2<0;⑤x1>|x2|.
其中能使f(x1)<f(x2)恒成立的条件序号是________.(写出所有正确条件的序号)
②⑤
分析:先判断函数为偶函数,再考虑函数在 上的单调性,然后利用单调性的定义验证正确的条件,列举反例判断不正确的条件即可
上的单调性,然后利用单调性的定义验证正确的条件,列举反例判断不正确的条件即可
解答:函数的定义域为 ,
,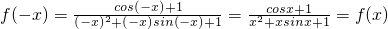
∴函数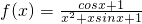 是偶函数
是偶函数
∴可先考虑函数在 上的单调性
上的单调性

=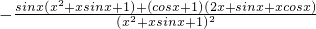
当 时,sinx≥0,cosx≥0,∴f′(x)<0
时,sinx≥0,cosx≥0,∴f′(x)<0
∴函数在 上的单调减
上的单调减
若x1>x2,取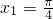 ,
,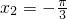 ,∴
,∴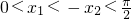 ,∴f(x1)>f(-x2),∴f(x1)>f(x2),∴①不正确;
,∴f(x1)>f(-x2),∴f(x1)>f(x2),∴①不正确;
若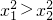 ,x1、x2∈
,x1、x2∈ ,∴
,∴ ≥|x1|>|x2|≥0,∴f(x1)<f(x2)恒成立,∴②正确;
≥|x1|>|x2|≥0,∴f(x1)<f(x2)恒成立,∴②正确;
若|x1|>x2,则取 ,
,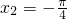 ,∴
,∴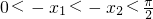 ,∴f(-x1)>f(-x2),∴f(x1)>f(x2),∴③不正确;
,∴f(-x1)>f(-x2),∴f(x1)>f(x2),∴③不正确;
若x1+x2<0,取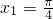 ,
,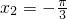 ,∴
,∴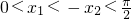 ,∴f(x1)>f(-x2),∴f(x1)>f(x2),可知④不正确
,∴f(x1)>f(-x2),∴f(x1)>f(x2),可知④不正确
若x1>|x2|,区间 上的任意实数x1、x2,即x1>x2,且x1,x2∈
上的任意实数x1、x2,即x1>x2,且x1,x2∈ ,,∴f(x1)<f(x2)恒成立,∴⑤正确;
,,∴f(x1)<f(x2)恒成立,∴⑤正确;
故答案为:②⑤
点评:本题以具体函数为载体,考查函数的性质,考查结论成立的条件,是个开放式的命题,对学生的理解判断能力要求比较高.
分析:先判断函数为偶函数,再考虑函数在
 上的单调性,然后利用单调性的定义验证正确的条件,列举反例判断不正确的条件即可
上的单调性,然后利用单调性的定义验证正确的条件,列举反例判断不正确的条件即可解答:函数的定义域为
 ,
,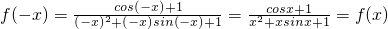
∴函数
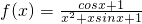 是偶函数
是偶函数∴可先考虑函数在
 上的单调性
上的单调性
=
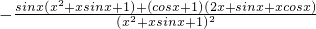
当
 时,sinx≥0,cosx≥0,∴f′(x)<0
时,sinx≥0,cosx≥0,∴f′(x)<0∴函数在
 上的单调减
上的单调减若x1>x2,取
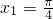 ,
,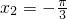 ,∴
,∴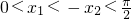 ,∴f(x1)>f(-x2),∴f(x1)>f(x2),∴①不正确;
,∴f(x1)>f(-x2),∴f(x1)>f(x2),∴①不正确;若
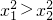 ,x1、x2∈
,x1、x2∈ ,∴
,∴ ≥|x1|>|x2|≥0,∴f(x1)<f(x2)恒成立,∴②正确;
≥|x1|>|x2|≥0,∴f(x1)<f(x2)恒成立,∴②正确;若|x1|>x2,则取
 ,
,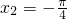 ,∴
,∴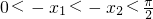 ,∴f(-x1)>f(-x2),∴f(x1)>f(x2),∴③不正确;
,∴f(-x1)>f(-x2),∴f(x1)>f(x2),∴③不正确;若x1+x2<0,取
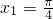 ,
,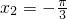 ,∴
,∴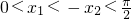 ,∴f(x1)>f(-x2),∴f(x1)>f(x2),可知④不正确
,∴f(x1)>f(-x2),∴f(x1)>f(x2),可知④不正确若x1>|x2|,区间
 上的任意实数x1、x2,即x1>x2,且x1,x2∈
上的任意实数x1、x2,即x1>x2,且x1,x2∈ ,,∴f(x1)<f(x2)恒成立,∴⑤正确;
,,∴f(x1)<f(x2)恒成立,∴⑤正确;故答案为:②⑤
点评:本题以具体函数为载体,考查函数的性质,考查结论成立的条件,是个开放式的命题,对学生的理解判断能力要求比较高.

练习册系列答案
相关题目
 ,则函数
,则函数 的图象不经过第三象限;
的图象不经过第三象限; 定义域是
定义域是 ,则
,则 的定义域是
的定义域是 ;
; 的单调减区间是
的单调减区间是
 ,那么
,那么 ;
; 是定义在
是定义在 上的不恒为
上的不恒为 的函数,且对于任意的
的函数,且对于任意的 ,都有
,都有 ,则函数
,则函数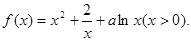
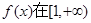 上单调递增,求a的取值范围;
上单调递增,求a的取值范围;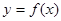 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式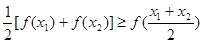 成立,则称函数
成立,则称函数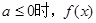 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
 满足
满足 ,对于任意
,对于任意 R都有
R都有 ,且
,且  ,令
,令 .
. 的表达式;
的表达式; 的单调区间;
的单调区间; 上的零点个数.
上的零点个数.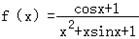 ,对于区间
,对于区间 上的任意实数x1、x2,有如下条件:
上的任意实数x1、x2,有如下条件: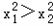 ;③|x1|>x2;④x1+x2<0;⑤x1>|x2|.
;③|x1|>x2;④x1+x2<0;⑤x1>|x2|.