题目内容
已知函数
 满足
满足 ,对于任意
,对于任意 R都有
R都有 ,且
,且  ,令
,令 .
.
(Ⅰ)求函数 的表达式;
的表达式;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)研究函数 在区间
在区间 上的零点个数.
上的零点个数.
∵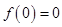 ,∴
,∴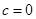 .
…… 1分
.
…… 1分
∵对于任意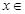 R都有
R都有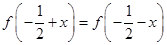 ,
,
∴函数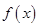 的对称轴为
的对称轴为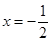 ,即
,即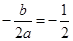 ,得
,得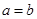 . …… 2分
. …… 2分
又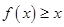 ,即
,即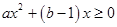 对于任意
对于任意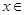 R都成立,
R都成立,
∴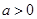 ,且
,且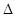
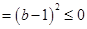 .
.
∵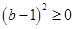 , ∴
, ∴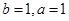 .
.
∴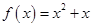 .
…… 4分
.
…… 4分
(2) 解: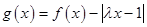
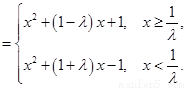 …… 5分
…… 5分
① 当 时,函数
时,函数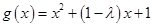 的对称轴为
的对称轴为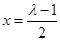 ,
,
若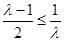 ,即
,即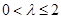 ,函数
,函数 在
在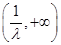 上单调递增; …… 6分
上单调递增; …… 6分
若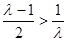 ,即
,即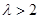 ,函数
,函数 在
在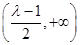 上单调递增,在
上单调递增,在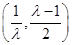 上单调递减. …… 7分
上单调递减. …… 7分
② 当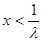 时,函数
时,函数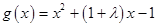 的对称轴为
的对称轴为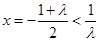 ,
,
则函数 在
在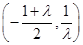 上单调递增,在
上单调递增,在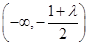 上单调递减. …… 8分
上单调递减. …… 8分
综上所述,当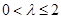 时,函数
时,函数 单调递增区间为
单调递增区间为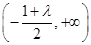 ,单调递减区间为
,单调递减区间为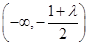 ;
…… 9分
;
…… 9分
当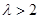 时,函数
时,函数 单调递增区间为
单调递增区间为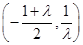 和
和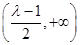 ,单调递减区间为
,单调递减区间为
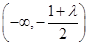 和
和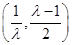 .
…… 10分
.
…… 10分
(3)解:①
当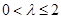 时,由(2)知函数
时,由(2)知函数 在区间
在区间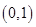 上单调递增,
上单调递增,
又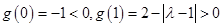 ,
,
故函数 在区间
在区间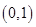 上只有一个零点. …… 11分
上只有一个零点. …… 11分
② 当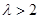 时,则
时,则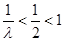 ,而
,而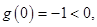
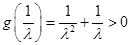 ,
,
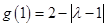 ,
,
(ⅰ)若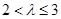 ,由于
,由于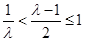 ,
,
且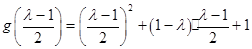
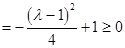 ,
,
此时,函数 在区间
在区间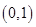 上只有一个零点;
…… 12分
上只有一个零点;
…… 12分
(ⅱ)若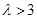 ,由于
,由于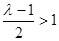 且
且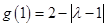
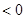 ,此时,函数
,此时,函数 在区间
在区间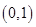 上有两个不同的零点.
…… 13分
上有两个不同的零点.
…… 13分
综上所述,当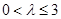 时,函数
时,函数 在区间
在区间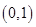 上只有一个零点;
上只有一个零点;
当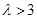 时,函数
时,函数 在区间
在区间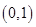 上有两个不同的零点.
上有两个不同的零点.
【解析】略

 全能练考卷系列答案
全能练考卷系列答案[番茄花园1] 本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分10分。
若实数 、
、 、
、 满足
满足 ,则称
,则称 比
比 远离
远离 .
.
(1)若 比1远离0,求
比1远离0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、 ,证明:
,证明: 比
比 远离
远离 ;
;
(3)已知函数 的定义域
的定义域 .任取
.任取 ,
, 等于
等于 和
和 中远离0的那个值.写出函数
中远离0的那个值.写出函数 的解析式,并指出它的基本性质(结论不要求证明).
的解析式,并指出它的基本性质(结论不要求证明).
23本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知椭圆 的方程为
的方程为 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足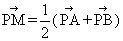 ,求点
,求点 的坐标;
的坐标;
(2)设直线 交椭圆
交椭圆 于
于 、
、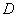 两点,交直线
两点,交直线 于点
于点 .若
.若 ,证明:
,证明: 为
为 的中点;
的中点;
(3)对于椭圆 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆 上存在不同的两个交点
上存在不同的两个交点 、
、 满足
满足 ,写出求作点
,写出求作点 、
、 的步骤,并求出使
的步骤,并求出使 、
、 存在的θ的取值范围.
存在的θ的取值范围.
[番茄花园1]22.
 上的函数
上的函数 满足条件:存在实数
满足条件:存在实数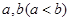 且
且

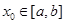 ,有
,有 (
( 是常数);
是常数); ,当
,当 ,总有
,总有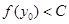 。
。 称为“平顶型”函数,称
称为“平顶型”函数,称 为“平顶宽度”。根据上述定义,解决下列问题:
为“平顶宽度”。根据上述定义,解决下列问题: 是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。
是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由。 是“平顶型”函数,求出
是“平顶型”函数,求出 的值。
的值。 在
在 上有两个不相等的根,求实数
上有两个不相等的根,求实数 的取值范围。
的取值范围。 ,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;
,3},则使函数y=xa的定义域为R且该函数为奇函数的所有a的值为1,3;