Question

如图，在直三棱柱ABC—A₁B₁C₁中，BA=BC=2，·=0，异面直线A₁B与AC成60°的角，点O、E分别是棱AC和BB₁的中点，点F是棱B₁C₁上的动点.

（1）证明：A₁E⊥OF；

（2）求点E到面AB₁C的距离；

（3）求二面角B₁—A₁C—C₁的大小.

Answer 1

解：（1）设棱柱的高为h，以B为坐标原点，以BA、BC、BB₁所在直线为x、y、z轴建立空间直角坐标系，则A（2，0，0），C（0，2，0），O（1，1，0），A₁（2，0，h），

∴=(2,0,h)，=（2，-2，0），

∴cos(,)=,

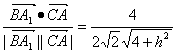即cos60°=,

解得h=2.

∴E(0,0,1),A₁(2,0,2),

∴=(-2,0,-1).

∵F是B₁C₁上的动点，

∴设F（0，y，2），

∴=（-1，y-1，2），

∴·=（-2，0，-1）·（-1，y-1，2）=0，

∴⊥，即A₁E⊥OF.

（2）易求面AB₁C的法向量为n=(1,1,1)，=（2，0，-1），

所以E到面AB₁C的距离为

d=.

（3）∵平面A₁CC₁的一个法向量是=（1，1，0）.

设平面A₁B₁C的一个法向量是

n=(x,y,z),=(-2,2,-2)

=(-2,0,0),

则n·=(x,y,z)·(-2,2,-2)

=-2x+2y-2z=0,①

n·=(x,y,z)·(-2,0,0)

=-2x=0,∴x=0.②

代入①并令z=1得y=1,∴n=(0,1,1),

∴cos(n，)=，

∴(n，)=60°，

即二面角B₁-A₁C-C₁的大小为60°.