题目内容
在任意两个正整数m、n间定义某种运算(用
解析:可分三类:第一类:a,b全为正偶数,则(a,b)可以是(34,2),(32,4),(30,6),…,(2,34),共计17个;
第二类:a,b全为正奇数,则(a,b)可以是(35,1),(33,3),…,(1,35)共计18个;
第三类:a,b中一个正奇数,一个正偶数,则(a,b)可以是(4,9),(9,4),(12,3),(3,12),(36,1),(1,36)共计6个;
由加法原理可知集合中共有元素:N=17+18+6=41(个).

练习册系列答案
相关题目
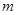 ※
※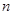 =
=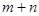 当
当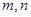 中一个为正偶数,另一个为正奇数时,
中一个为正偶数,另一个为正奇数时,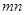 .则在此定义下,集合
.则在此定义下,集合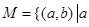 ※
※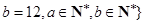 中的元素个数是( )
中的元素个数是( )