题目内容

在任意两个正整数m、n间定义某种运算(用表示运算符号)：当m、n都为正偶数或都为正奇数时，mn=m+n，如46=4+6=10，37=3+7=10，当m、n中一个为正奇数，另一个为正偶数时，mn=mn，如34=3×4=12，43=4×3=12.则在上述定义下，集合M=｛(a,b)|ab=36，a、b∈N｝中的元素个数为_________.

思路解析：在充分理解题目中给出的新的定义的基础上，利用所学的知识求解.

分两类：①当m、n都为正偶数或都为正奇数时：

∵mn=m+n=36，∴m=1，n=35；m=2，n=34;m=3，n=33；…；m=35，n=1,集合M共有35个元素.

②当m、n一个为正偶数，一个为正奇数时，mn=m·n=36.

又∵1×36=36，3×12=36,4×9=36，

∴故M中有6个元素.综上M中共有6+35=41个元素.

答案：41

练习册系列答案
相关题目
有下列叙述
①集合A=（m+2，2m-1）⊆B=（4，5），则m∈[2，3]
②两向量平行，那么两向量的方向一定相同或者相反
③若不等式(-1)na＜2+
(-1)n+1
n
对任意正整数n恒成立，则实数a的取值范围是[-2，
3
2
)
④对于任意两个正整数m，n，定义某种运算⊕如下：
当m，n奇偶性相同时，m⊕n=m+n；当m，n奇偶性不同时，m⊕n=mn，在此定义下，集合M={（a，b）|a⊕b=12，a∈N+，b∈N+}中元素的个数是15个．
上述说法正确的是
③，④
③，④
．
（2013•惠州模拟）对于任意两个正整数m，n，定义某种运算“※”如下：当m，n都为正偶数或正奇数时，m※n=m+n；当m，n中一个为正偶数，另一个为正奇数时，m※n=mn．则在此定义下，集合M={（a，b）|a※b=12，a∈N*，b∈N*}中的元素个数是（　　）
在任意两个正整数m、n间定义某种运算（用表示运算符号）.当m、n都为正偶数或都为正奇数时，mn=m+n,如46=4+6=10;37=3+7=10.当m、n中一个为正奇数，另一个为正偶数时，mn=mn,如34=3×4=12;43=4×3=12,则上述定义下，集合M={（a,b）|ab=36,a、b∈N*}中元素的个数为_____________.

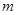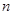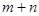对于任意两个正整数m, n , 定义某种运算“※”如下：当m ,n都为正偶数或正奇数时,※=当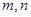中一个为正偶数,另一个为正奇数时,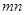※=.则在此定义下,集合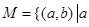※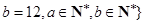中的元素个数是(     )

A.10个          B.15个           C.16个             D.18个

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网